Предмет: Математика,
автор: Мигель7
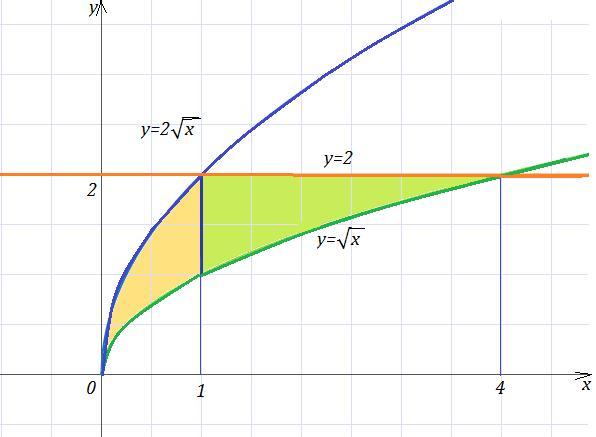
Вычислить площадь фигуры, ограниченной линиями с помощью определённого интеграла, сделать иллюстрацию y=√x, y=2√x, y=2.
Ответы
Автор ответа:
0
Ответ:
площадь==============================================
Пошаговое объяснение:
Приложения:

Автор ответа:
0
Точки пересечения:
Приложения:
Похожие вопросы
Предмет: Биология,
автор: sofiaivanova501
Предмет: Химия,
автор: vanyabondar2006
Предмет: Математика,
автор: ogilmanova00
Предмет: Математика,
автор: Alena26032007
Предмет: Математика,
автор: cooljojo2017