Перпендикуляр, опущений з точки кола на його діаметр, ділить діаметр на відрізки, різниця яких дорівнює 5 см. знайдіть радіус кола, якщо довжина перпендикуляра дорівнює 6 см.
Ответы
Перпендикуляр, опущенный из точки окружности на диаметр. делит его на отрезки. разность длин которых равна 5 см. Найдите радиус окружности, если длина перпендикуляра равна 6 см.
————————————
Ответ: 6,5 см
Объяснение:
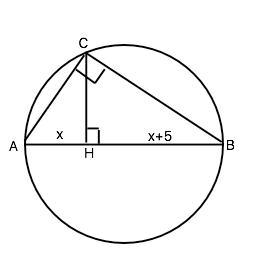
Обозначим диаметр АВ, точку на окружности - С. Перпендикуляр СН будет высотой прямоугольного треугольника АСВ с углом С=90°, т.к. вписанный угол АСВ опирается на диаметр.
Примем длину отрезка АН=х, тогда ВН=х+5
Высота прямоугольного треугольника из прямого угла есть среднее пропорциональное между отрезками, на которые она делит гипотенузу. ⇒
СН²=АН•ВН ⇒ 36=х•(х+5), откуда получим квадратное уравнение х²+5х-36=0
По т.Виета
сумма корней приведенного квадратного трехчлена x*²+ p x + q = 0 равна его второму коэффициенту с противоположным знаком, а произведение - свободному члену .
х₁+х₂= -5
х₁•х₂= -36
36=4•9. ⇒ х₁=-9, х₂=4 (-9+4=-5) Отрицательный корень отбрасываем.
Следовательно, х=4, х+5=9. Диаметр АВ=4+9=13, R=13:2=6,5 см
------------
Ясно, что найти корни уравнения можно через дискриминант с тем же результатом.