Предмет: Алгебра,
автор: Halier
помогите решить неравенство
Приложения:
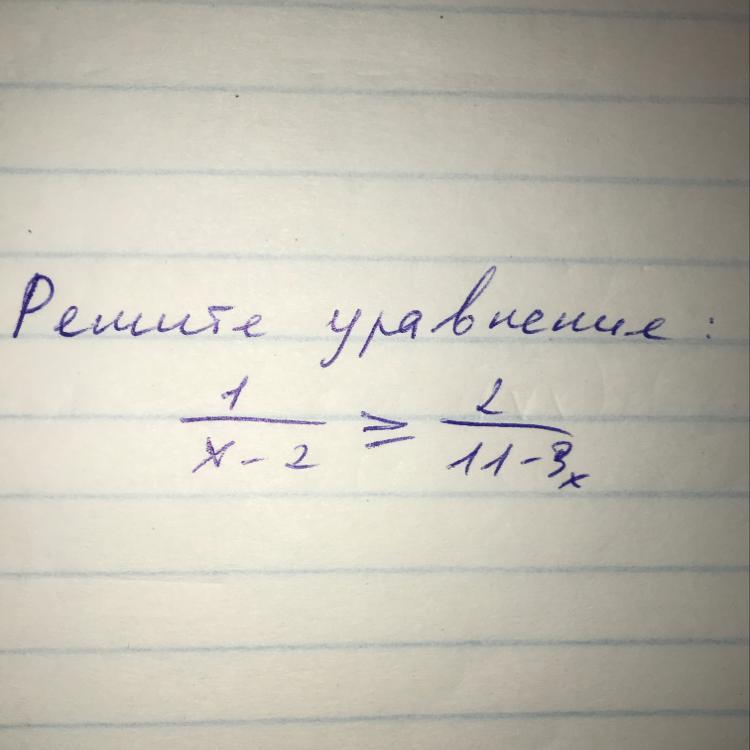
Universalka:
Это не уравнение, а неравенство .
Ответы
Автор ответа:
0
- + - +
__________(2)__________[3]___________(3 2/3)___________
//////////////////////// //////////////////////////
x ∈ (2 ; 3] ∪ (3 2/3 ; + ∞)
Скажите, а не нужно ОДЗ написать? Все же перенос скобок из знаменателя в числитель не является равносильным переходом
У меня ОДЗ учтено на рисунке, где нули знаменателя отмечены круглыми скобками.
Я же не говорю, что у Вас неправильный ответ. Но с формальной точки зрения у Вас есть неравносильный переход. Ребенок, который предлагает такую простую задачу, скорее всего не слишком хорошо разбирается в математике. Поэтому (по моему скромному мнению) указать ограничения в этот момент совершенно необходимо.
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: nikitastanok90
Предмет: История,
автор: iholaihola14052020
Предмет: Математика,
автор: Igorek13112004