Найдите область определения функции :
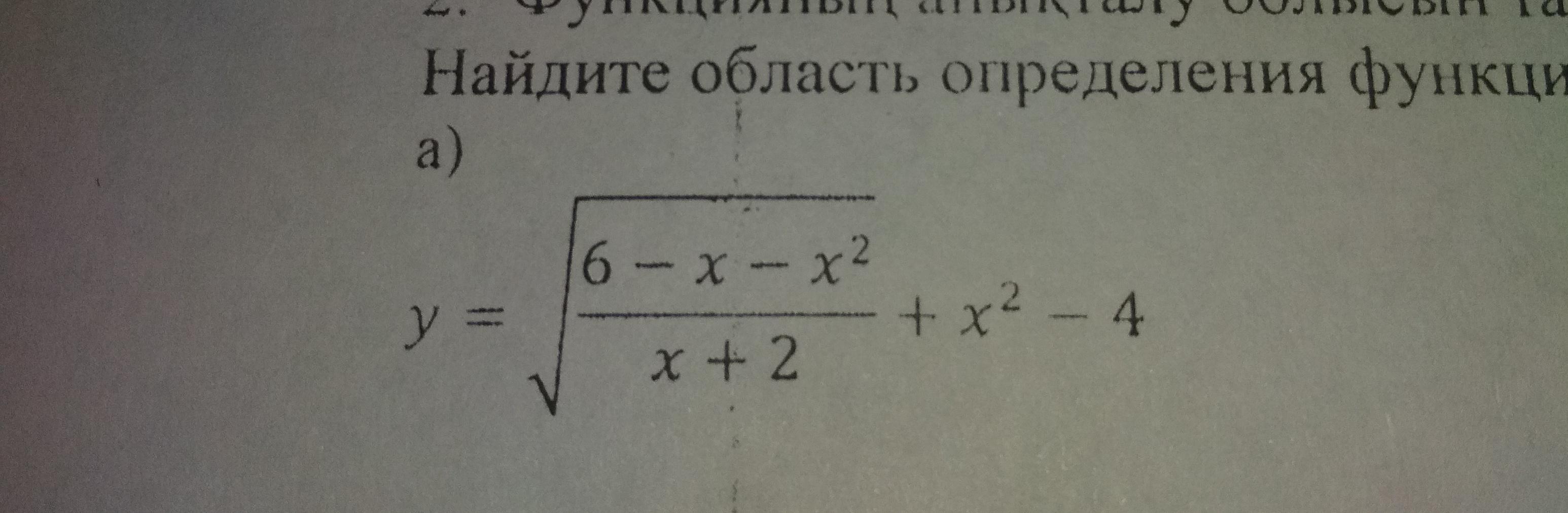
Ответы
Выражение, записанное под корнем чётной степени, должно быть неотрицательным, то есть ≥ 0 .
- + - +
_________[-3]__________(-2)__________[2]_________
//////////////////// /////////////////////////
Ответ : x ∈ (- ∞ ; - 3] ∪ (- 2 ; 2]
ПОДКОРЕННОЕ ВЫРАЖЕНИЕ НЕОТРИЦАТЕЛЬНО. ЭТО равносильно системе двух неравенств. а именно
(6-х-х²)(х+2)≥0
х+2≠0,
которая в свою очередь эквивалентна такой системе
(х²+х-6)(Х+2)≤0
х≠-2,первое неравенство решим методом интервалов. корни уравнения х²+х-6=0 по теореме. обратной теореме Виета равны -3 и 2. перепишем первое неравенство. разложив на множители первую скобку. как
(х-2)(х+3), а неравенство как (х-2)(х+3)(х+2)≤0
____-3___-2___________2___________________
+ - + -
Решением которого будет х∈[-3;-2)∪[2;+∞)