Предмет: Алгебра,
автор: Alizhmen
Плизз хелп ми. Очень надо
Приложения:
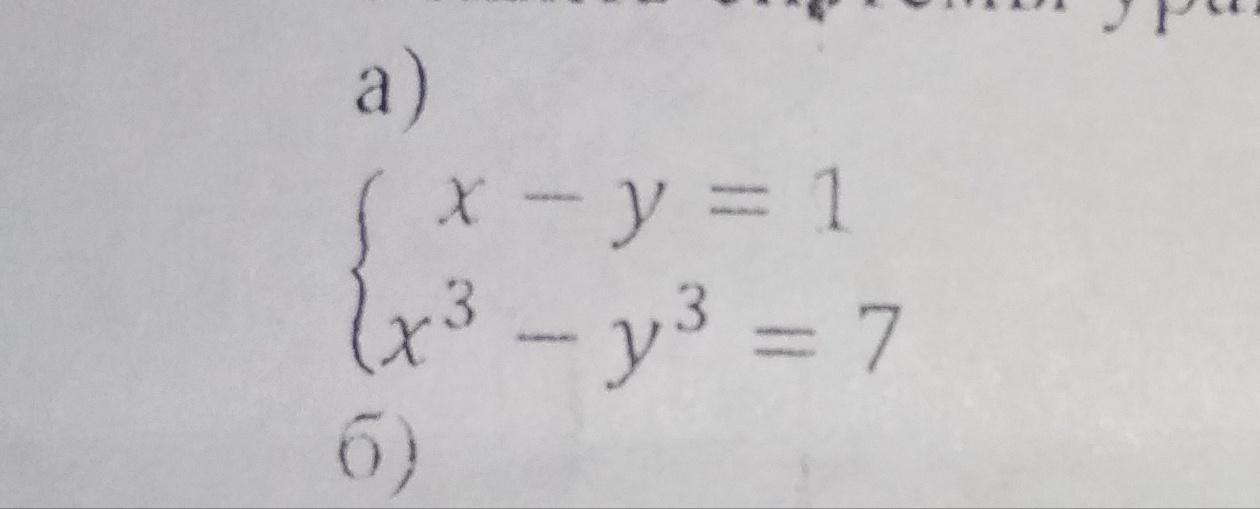
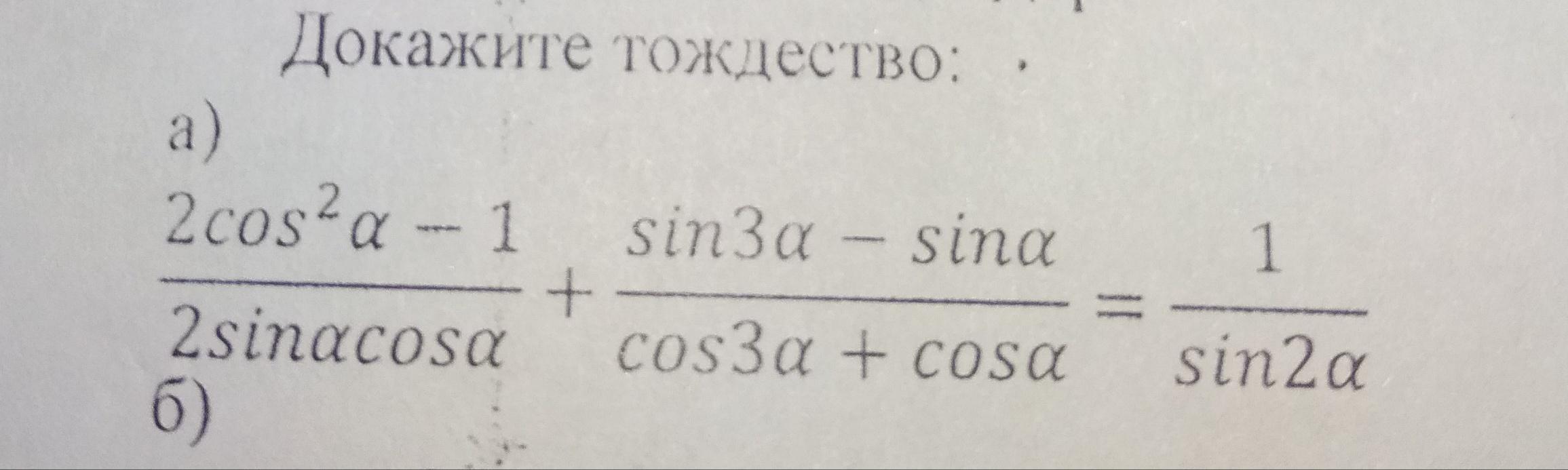
Ответы
Автор ответа:
1
Тождество доказано
Похожие вопросы
Предмет: Литература,
автор: kamilasaska874
Предмет: Алгебра,
автор: comfylenovo3
Предмет: Алгебра,
автор: ank09744789
Предмет: Физика,
автор: Smr199876
Предмет: История,
автор: бабик1