Предмет: Математика,
автор: мороженкаAikas
Найти общее решение дифференциального уравнения
Приложения:
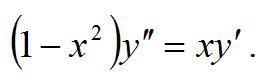
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: sergijgostuk19
Предмет: Английский язык,
автор: neymarpliska11
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: зали6
Предмет: Математика,
автор: BigRussianBoss51