Как они получили такой график (график функции с системой уравнений и модулями)?

Ответы
Ответ:
Объяснение:
=================
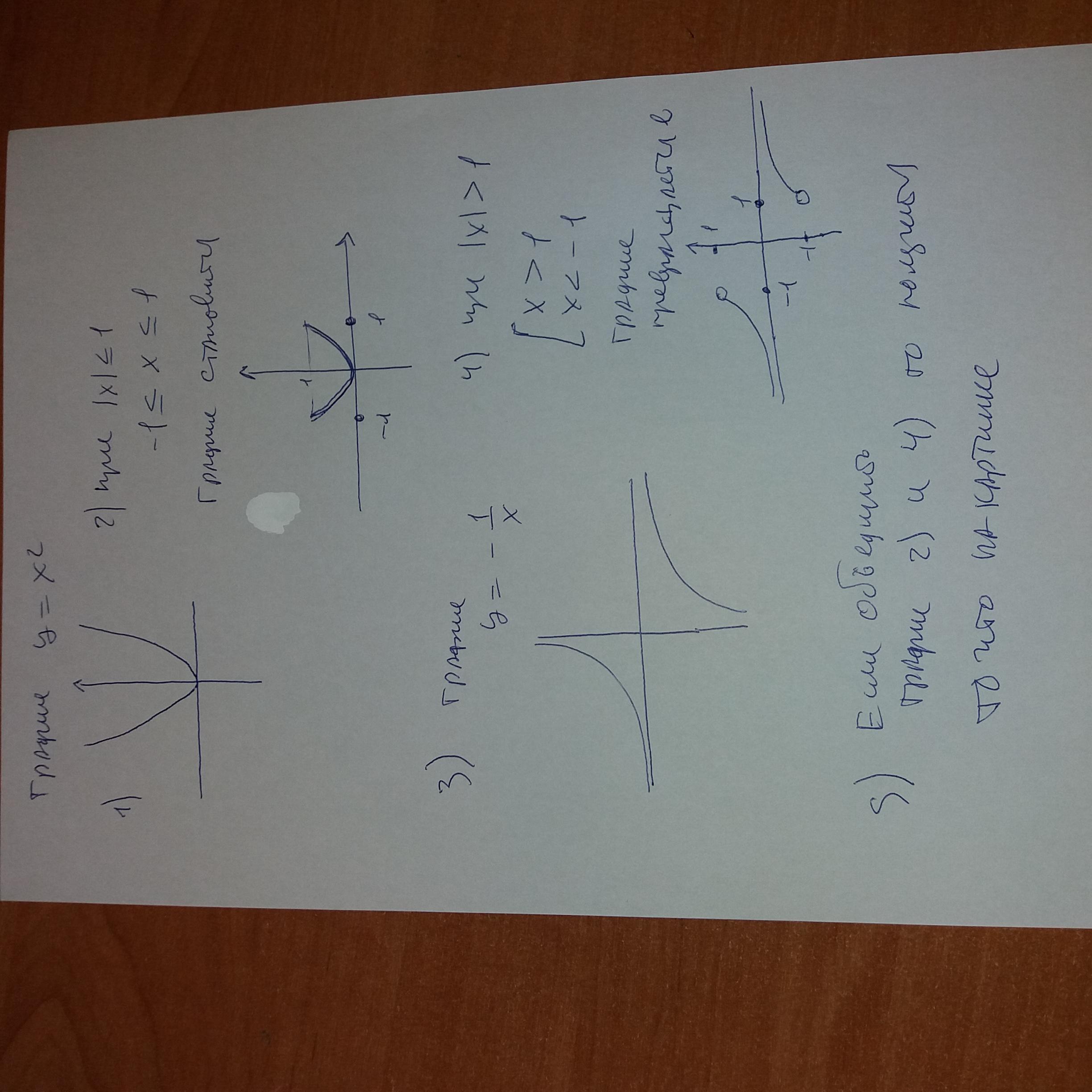
Обратите внимание на то\. где задана эта функция. область ее определения разбита на три кусочка\. на отрезке [-1;1], а это и есть условие модуль икс меньше или равен единицы, это обычная парабола, на рисунке она показана именно на этом участке\. а вне этого отрезка, т.е. правее единицы и левее минус единицы это и есть модуль икс больше единицы\. у вас две веточки гиперболы. обратите внимание\. неравенство строгое. поэтому точка (1;-1) выколота. а вот точка (-1;1) закрашена, или полная.\ за счет того. что парабола в этой точке определена. Далее. прямая у=с- это прямая. параллельная оси ох, поднимите ее от минус бесконечности до минус единицы. там у графика функции этой прямой вообще нет общих точек. если вы поднимете ее от -1 до нуля, не включая ноль и минус один. то у вас будет одна точка пересечении\ прямой у=с и гиперболы, а если поднят ь прямую выше. то именно в точке ноль у нее с параболой уже одна общая точка. дальше от нуля до единицы у них три точки пересечени\. а выше единицы. общих точек вовсе нет. Ясно?