Предмет: Геометрия,
автор: iukaktus
Стороны основания треугольной пирамиды,объем которой 2000см3, равны 20 см,30 см,40 см. Боковые ребра пирамиды равнонаклонены к плоскости основания. Вычислите угол между боковым ребром и плоскостью основания.
Ответы
Автор ответа:
1
Ответ: 45°
Объяснение:
Если боковые ребра пирамиды равнонаклонены, т.е. угол наклона к основанию всех ребер одинаков, то её высота проходит через центр описанной около основания окружности.
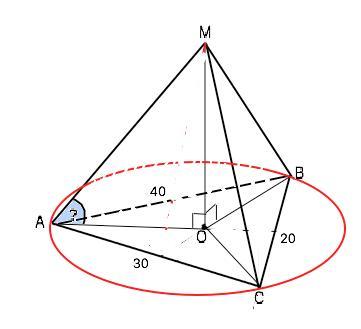
Пусть в пирамиде МАВС МО - высота, АВ=40 см, ВС=20 см, АС=30 см. АО=ВО=СО=R.
Полупериметр ∆ АВС=45
Найденная по формуле Герона Ѕ(АВС)=√(45•5•15•25)=75√15.
Формула радиуса описанной около треугольника окружности R=a•b•c/4S, где a,b,c - стороны треугольника, S- его площадь.
R=(20•30•40):(4•75√15)=80/√15
Формула объема пирамиды V=h•S/3 ⇒ 2000=(h•75√15):3. Решив уравнение, получим h=80/√15
В прямоугольном треугольнике АSО катеты АО=SО=80√15. ⇒ tg(SAO)=1. Угол SAO=45°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: grebenukangelina49
Предмет: Қазақ тiлi,
автор: yakimovaeva2018
Предмет: Биология,
автор: prudden85
Предмет: Математика,
автор: katyateplyansk
Предмет: Математика,
автор: Аноним