Предмет: Алгебра,
автор: fqrfhkb49
Помогите решить неравенство
Приложения:
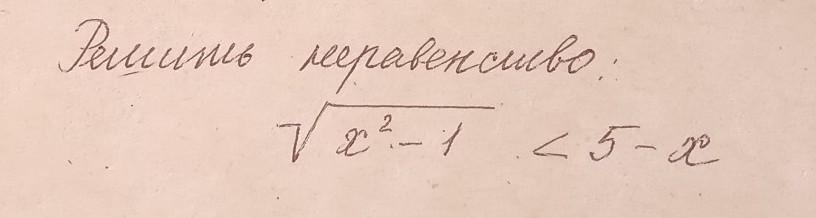
Ответы
Автор ответа:
1
1) ОДЗ:
Общее решение для ОДЗ:
2) Возведем обе части данного неравенства в квадрат:
3) С учетом ОДЗ получаем общее решение:
Ответ: х ∈ (-∞; -1]∪[1; 2,6)
Похожие вопросы
Предмет: Русский язык,
автор: evgenijzdorikov
Предмет: История,
автор: qwerty5656099
Предмет: Биология,
автор: abdrahmanovaul11
Предмет: Математика,
автор: Crystallyna