Предмет: Математика,
автор: 2000denis
Помогите с дифференциальным уравнением
Приложения:
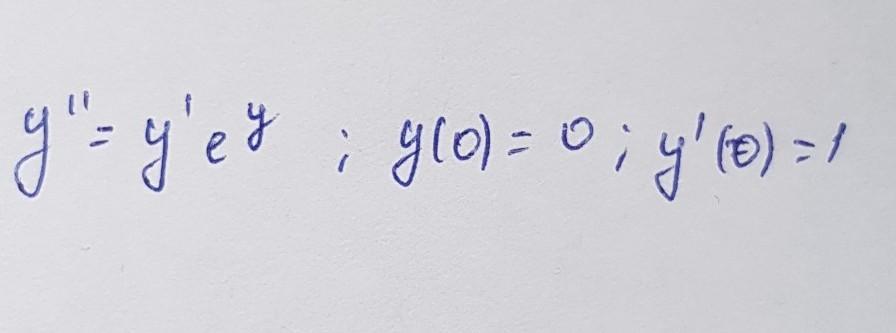
Ответы
Автор ответа:
0
Исспользуем подстановку:
Тогда получим:
и уравнение запишется в виде:
Данное дифференциальное уравнение также будет иметь особое решение:
Чтобы найти решение данной задачи Коши, нужно подставить в равенства
и
соответствующие начальные условия.
2000denis:
а это разве все?
А можешь еще одно дифференциальное уравнение решить, посмотри в заданиях
прошу прощения но в этом дифуре, если подставить начальные условия, выходит неопределенность
Похожие вопросы
Предмет: Информатика,
автор: 152386947kx
Предмет: Русский язык,
автор: nerp208
Предмет: География,
автор: mensikovamilana775
Предмет: Алгебра,
автор: Макс5163
Предмет: Информатика,
автор: ANDRECASER