Предмет: Геометрия,
автор: bogyu
СРОЧНО
на экще помогите люди добрые
Приложения:
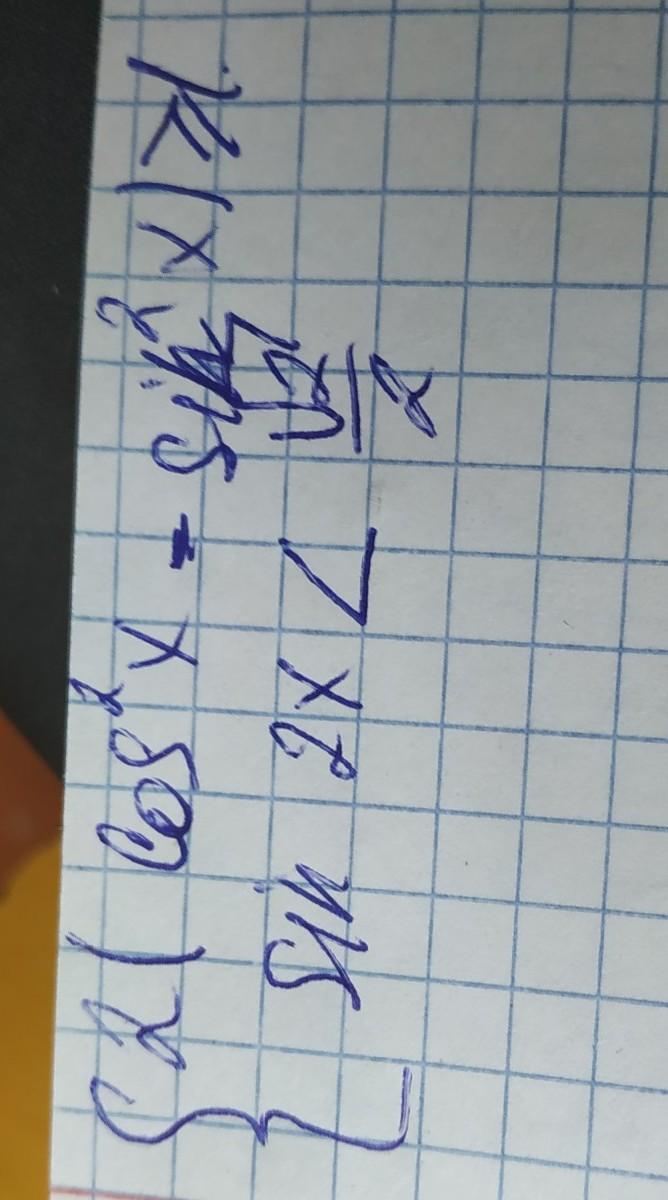
Ответы
Автор ответа:
1
1) cos²x-sin²x = cos²x - (1-cos²x)
Раскроем скобки: cos²x - 1 + cos²x
2cos²x-1 = cosx(cosx - 1)
cosx(cosx - 1) = 0
cosx = x + = 0
cosx - 1 = 0
cosx = 1
x = 2πn, n ∈ Z. Два ответа. При умножении - 0.
2) sin 2x = 2 * sinα cosα
2 * sinα cosα <
2 * 0 * (-1) <
0 <
Получаем:
С первым решением не выйдет - знак противоречия. Во втором всё верно, если 3,14 разделить на 4. Пишем ответ.
0 <
0 < 0,785
x = 0, так как деление и умножение на ноль не выйдет.
Ответ: 0.
bogyu:
лав ю
Похожие вопросы
Предмет: Химия,
автор: koval436
Предмет: Українська мова,
автор: mariaudovkina359
Предмет: Английский язык,
автор: tokyo86
Предмет: Математика,
автор: nasr2006
Предмет: Математика,
автор: KORESHKIN