Question

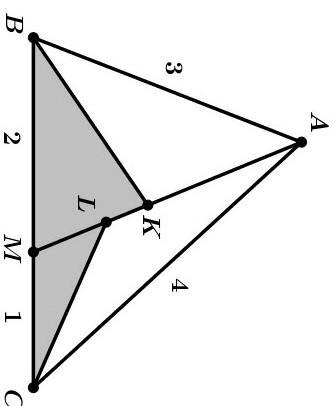
На стороне BC треугольника ABC выбрана точка M. Биссектрисы углов B и C пересекают отрезок AM в точках K и L соответственно. Известные длины отрезков изображены на рисунке. Найдите отношение площади треугольника BKM к площади треугольника CLM.
Срочно пж
Заранее благодарю.​

Answer 1

Ответ: 4/1.

Объяснение:

По свойству биссектрисы треугольника имеем:

AK/KM = AB/BM = 3/2,

AL/LM = AC/CM = 4/1,

Кроме того:

S(ABK)/S(BKM) = (0,5*h*AK)/(0,5*h*KM) = AK/KM = 3/2,

то есть S(ABK) = (3/2)*S(BKM).

S(ACL)/S(CLM) = (0,5*h*AL)/(0,5*h*LM) = AL/LM = 4/1 = 4,

то есть S(ACL) = 4*S(CLM),

S(ABM)/S(ACM) = (0,5*h*BM)/(0,5*h*CM) = BM/CM = 2/1 = 2.

Кроме того: S(ABM) = S(ABK) + S(BKM)

S(ACM) = S(ACL) + S(CLM),

поэтому

( S(ABK) + S(BKM) )/( S(ACL) + S(CLM) ) = 2,

( (3/2)*S(BKM) + S(BKM) )/( 4*S(CLM) + S(CLM) ) = 2,

( (5/2)*S(BKM) )/( 5*S(CLM) ) = 2,

( (1/2)*S(BKM) )/S(CLM) = 2,

S(BKM)/S(CLM) = 2*2 = 4.