Question

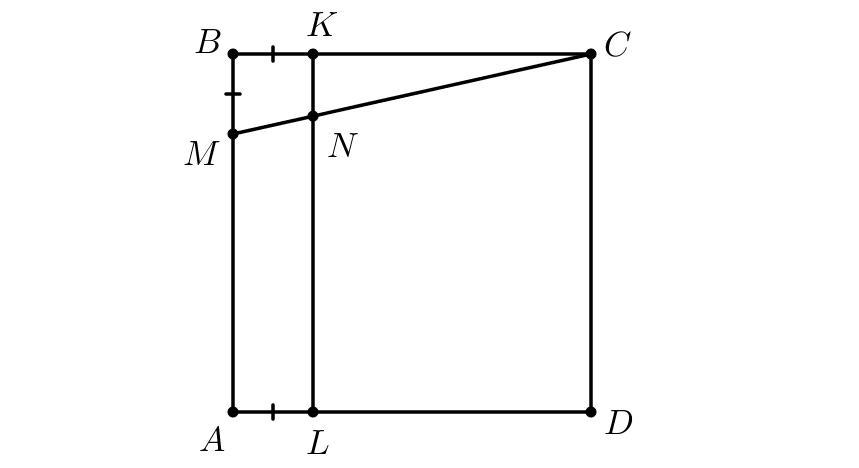
На сторонах AB, BC и AD квадрата ABCD выбраны точки M, K, L соответственно так, что AL=BM=BK. Отрезки KL и CM пересекаются в точке N. Выберите 4 точки, являющиеся вершинами треугольника и его ортоцентром соответственно.

Answer 1

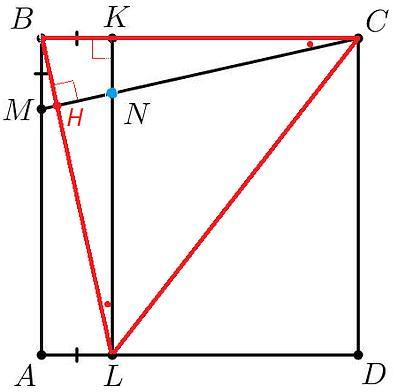
H - точка пересечения BL и CM.

AD||BC, AL=BK => ABKL - параллелограмм, AB||LK, AB=LK

AB⊥BC => LK⊥BC, ∠LKB=90

AB=BC => LK=BC

△MCB=△BLK (по двум катетам), ∠MCB=∠BLK

△BCH~△BLK (по двум углам, ∠LBC - общий), ∠CHB=∠LKB=90

Треугольник LBC, LK и CH - высоты, N - ортоцентр (точка пересечения высот, высоты треугольника пересекаются в одной точке).