Question

Діагональ рівнобічної трапеції є бісектрисою тупого кута і ділить середню лінію на відрізки 3 см і 13 см. Знайдіть периметр і площу трапеції.





​

Answer 1

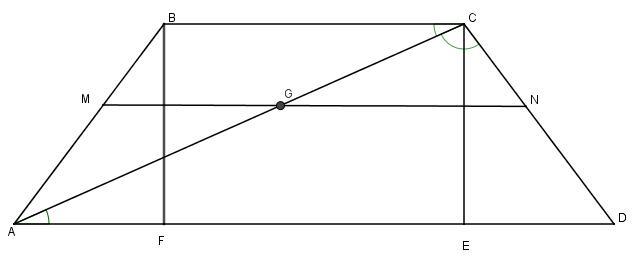
MG - середня лінія трикутника ABC ⇒ BC = 2MG = 2·3 = 6 см

NG - середня лінія трикутника ACD ⇒ AD = 2NG = 2·13 = 26 см

Оскільки АС - бісектриса кута ВСD, то ∠BCA = ∠ACD.

∠CAD = ∠BCA як навхрест лежащі кути при AD || BC і січній AC

Звідси ΔACD — рівнобедрений ⇒ AD = CD = 26 см.

AF = ED = (AD - BC)/2 = (26 - 6)/2 = 10

З прямокутного трикутника CED: за теоремою Піфагора:

$CE=\sqrt{CD^2-ED^2}=\sqrt{26^2-10^2}=24$ см

$S_{ABCD}=\dfrac{AD+BC}{2}\cdot CE=\dfrac{26+6}{2}\cdot 24=384$ см²

$P_{ABCD}=AD+BC+CD+AB=26+6+26+26=84$ см