Предмет: Геометрия,
автор: sasha63847
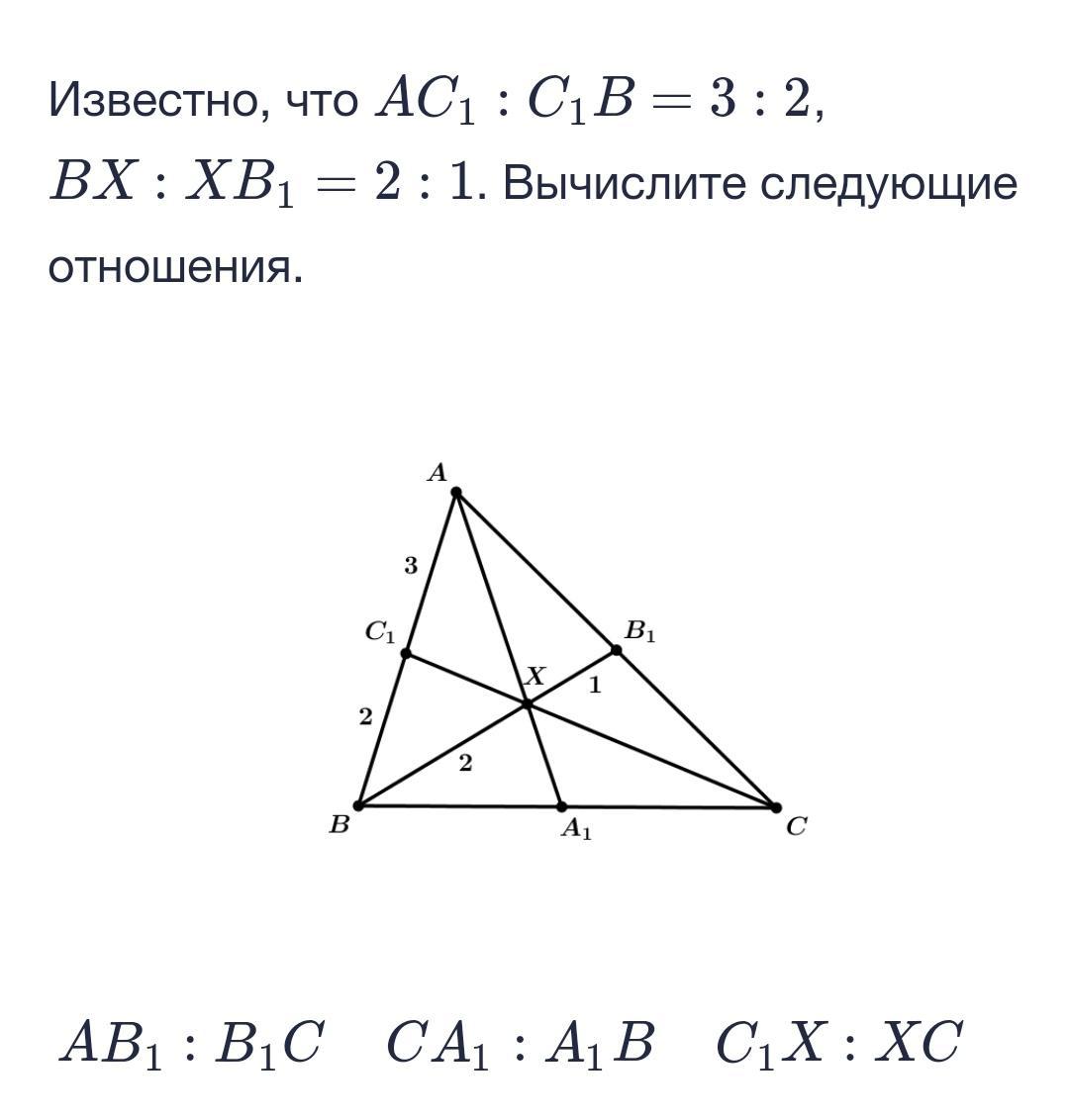
Памагите!!! Восьмой раз задаю этот вопрос. 500 баллов в пустую!!!
Приложения:
mathgenius:
Удобно решать через отношения площадей.
Тогда не нужно проводить вспомогательные параллельные прямые
а еще можно Менелая , Ван - Обеля , Чеву использовать , ну и центр масс
не дождался решения через площади , придется самому делать
Как через теорему Чевы я и сам знаю. Через площади получилось громоздкое выражение. Лень было выражать одно через другое. Видимо не самый быстрый способ.
Пришла другая идея. Соединить С!
Соединить С1A1B1 в один треугольник. Так будет проще преобразовывать
Ответы
Автор ответа:
5
Ответ:
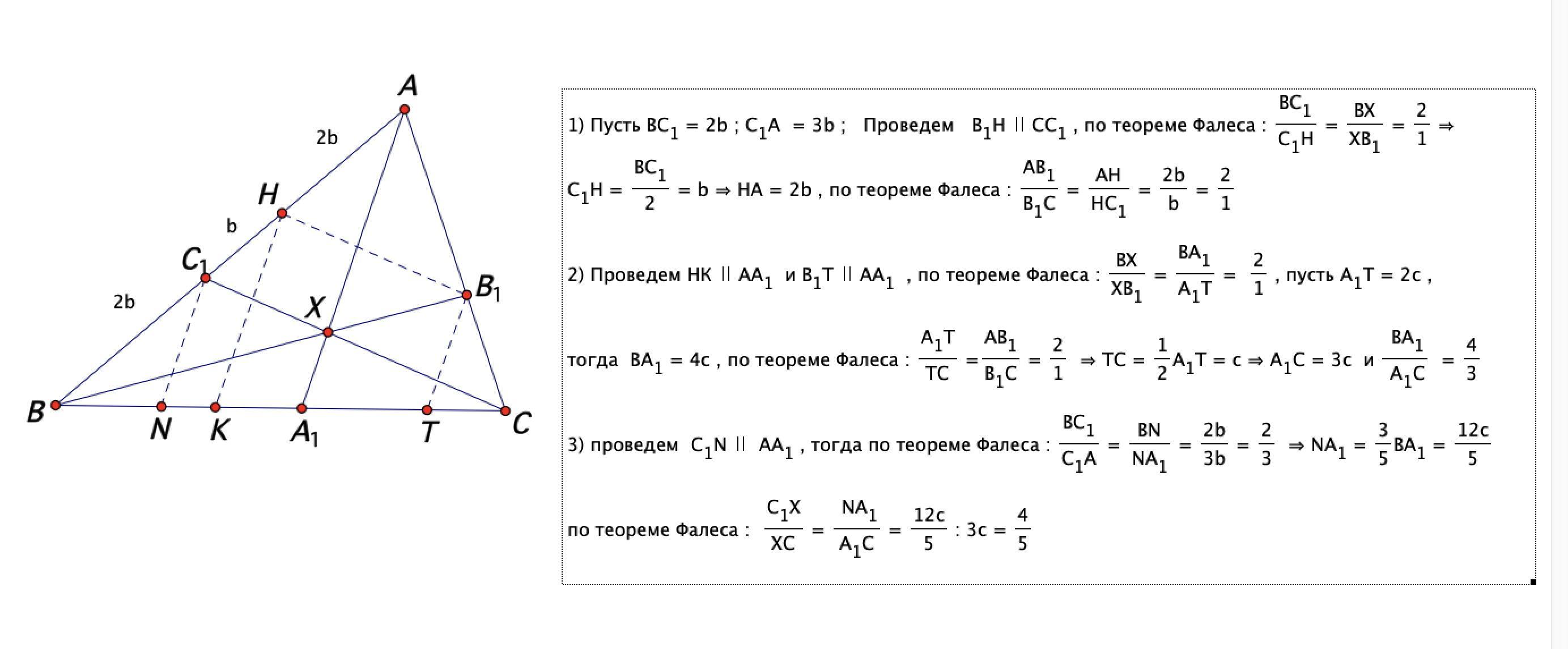
2 решения , второе очень школьное , добавил еще одно решение ( с площадями )
Объяснение: Решение :
Приложения:


А самое простое решение по моей любимой теореме Ван - Обеля , но школьники о ней , наверно вообще не слышали
Спасибо ,что не потрудились еще решение написать.
не поленились*
получилось с площадями , если получится выложу еще 2 решения
еще одно решение ( через площади )
Приятно на просторах сайта встретить любителя теоремы Ван-Обеля! Кстати, я про эту теорему узнал благодаря книге Понарина
Тоже знал ее. Но я стараюсь для школьников не использовать доп теоремы про отношения .
Хотя если два решения добавить как вы, то почему бы и нет. Для школьников полезно узнать что то новое .Это я только поощряю.
Даже 3, это ещё лучше!
Теорема Менелая очень хорошо работает в стереометрии ( задача № 14 ) , когда надо определить положение точки на ребре многогранника , проводить параллельные и играть площадями на ЕГЭ просто нет времени
Похожие вопросы
Предмет: Математика,
автор: baskova2012
Предмет: Геометрия,
автор: 666hello
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: 008ник
Предмет: Литература,
автор: alisa1410