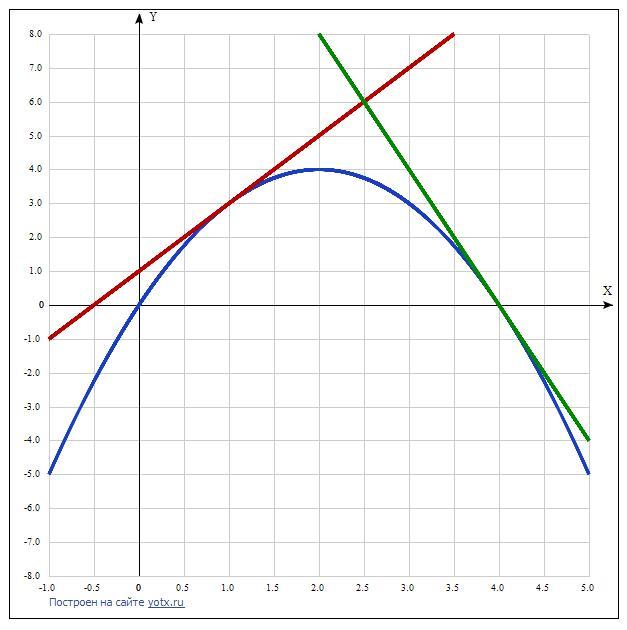
К графику функции f(x)=4x-x^2 проведены касательные в точках с абциссами х1=1 и х2=4 .найдите площадь треугольника, образованного этими касательными с осью Ох
Ответы
Производная функции f(x)=4x-x^2 равна y' = 4 - 2x.
Находим уравнения касательных для точек х1 = 1 и х2 = 4.
х1 = 1. y'(1) = 4-2 = 2, y(1) = 4 - 1 = 3. yкас = 2(х - 1) + 3 = 2х + 1.
х2 =4. y'(1) = 4-8 = -4, y(1) = 16 - 16 = 0. yкас = -4(х - 4) + 0 = -4х + 16.
Находим координаты точки А пересечения касательной от х1 с осью Ох. 2х + 1 = 0, х = -1/2. Точка А((-1/2; 0).
Находим координаты точки В пересечения двух касательных между собой. 2х + 1 = -4х + 16, 6х =15, х = 15/6 = 5/2 = 2,5. у = 2*2,5 + 1 = 6.
Точка В((2,5; 6).
Находим координаты точки С пересечения касательной от х2 с осью Ох. -4х + 16 = 0, х = 16/4 = 4. Точка С((4; 0).
Так как основание треугольника совпадает с осью Ох, то его длина равна 4 - (-1/2) = 4,5.
Высота треугольника равна координате точки В по оси Оу, то есть 6.
Получаем ответ: S = (1/2)*4,5*6 = 13,5 кв.ед.