Question

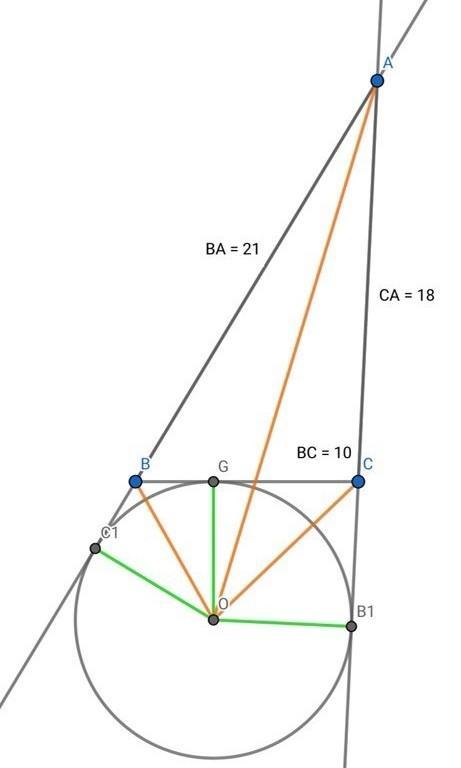
Вневписанная окружность треугольника ABC касается стороны BC в точке A1, а продолжений сторон AB и AC — в точках C1 и B1 соответственно. Известно, что AB=21, AC=18, BC=10. Вычислите длины следующих отрезков. AB1 CA1 BC1

Answer 1

Ответ:

24.5, 6.5, 3.5

Объяснение:

1)Пусть BC1 = x, CB1= y.

2)Т.к. отрезки касательных равны, то BA1 = BC1 = x, A1C = CB1 =y.

3)BA1+A1C=10 => x + y = 10

4)треугольник АОС1 равен треугольник АОВ1 по гипотенузе и острому углу => АС1 = АВ1, 21+х = 18+у

5) сост. и реш. сис. урав.

$\begin{cases}x + y = 10 \\ 21 + x = 18 + y \end{cases} \\ \begin{cases}x = 3.5 \\ y = 6.5 \end{cases}$

6)АВ1=18+у = 18 + 6.5 = 24.5

СА1 = y = 6.5

BC1 = x = 3.5

Update: на рисунке не G, а А1