Предмет: Алгебра,
автор: Tomoki
Найти экстремум функции двух переменных. Заранее спасибо.
Приложения:
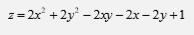
Ответы
Автор ответа:
1
Найдем частные производные по переменным x, y:
Приравниваем частные производные к нулю:
Вычислим теперь частные производные второго порядка для построения матрицы Гессиана:
В точке (1;-1) имеется минимум
Похожие вопросы
Предмет: География,
автор: dashakovach
Предмет: Математика,
автор: 5bratovk
Предмет: Литература,
автор: nastia3064
Предмет: Математика,
автор: sasandrey