Предмет: Алгебра,
автор: ЭрикаСыпко
Исследовать ряд на сходимость
Приложения:
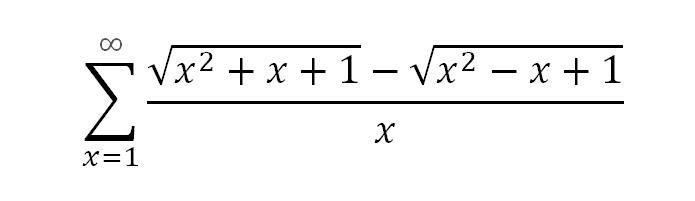
Ответы
Автор ответа:
1
Как известно, гармонический ряд расходится, а поскольку члены нашего ряда эквивалентны членам гармонического ряда, то и наш ряд расходится по признаку сравнения (напомню на всякий случай, что такой признак можно применять только для знакопостоянных рядов, попытка заменить члены знакопеременного ряда на эквивалентные члены может привести к неверным выводам).
Ответ: расходится
Похожие вопросы
Предмет: Математика,
автор: shlotgauereva
Предмет: Математика,
автор: maxzubko24
Предмет: Русский язык,
автор: Incognito599
Предмет: Обществознание,
автор: RovevaS
Предмет: История,
автор: NightLike