Question

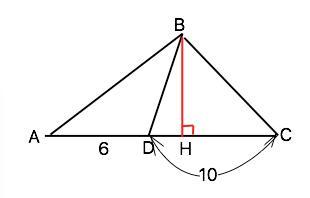
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.

Answer 1

Ответ: 30см²

Объяснение:

Высота ВН общая для треугольников  АВС, АВD и BDC.

Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты.

Ѕ(ABC):S(BCD)=AC:DC  

 Примем площадь ∆ BCD равной x ⇒

48:х=(6+10):10 => 480=16х ⇒ х=30 см²

Ответ: Ѕ(BCD)=30 см²

Тот же результат получим из отношения площадей треугольников АВС и BCD, выраженных по формуле S=a•h/2