Предмет: Алгебра,
автор: dermolaeva42
Как решить, помогите пжлст( желательно с пояснениями
Приложения:
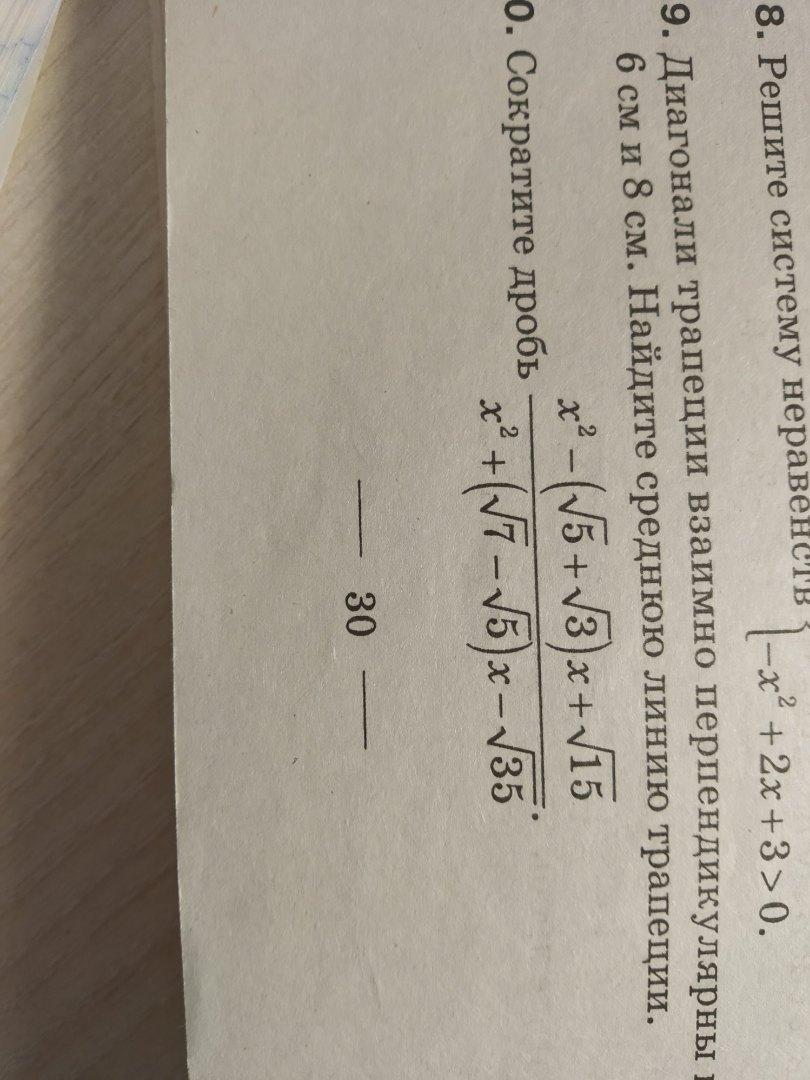
Ответы
Автор ответа:
0
1)
2)
3)
Ответ:
Приложения:
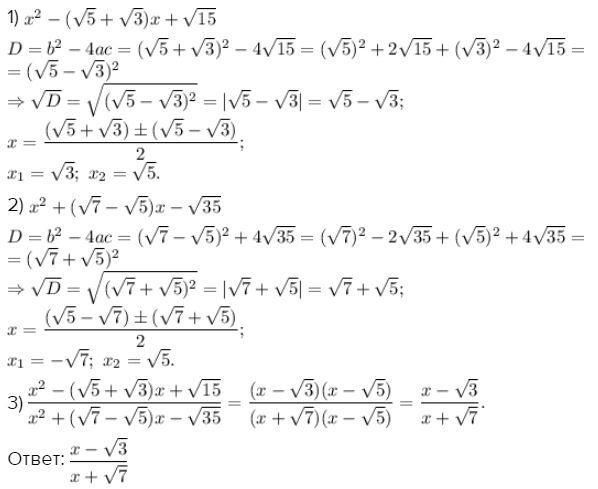
Похожие вопросы
Предмет: Математика,
автор: kushpilua66
Предмет: Геометрия,
автор: kozaku87
Предмет: Математика,
автор: annashinkarenko
Предмет: Математика,
автор: мери201
Предмет: Литература,
автор: Аноним