Предмет: Математика,
автор: alexs5655
Вычислите предел используя правила Лопиталя
Приложения:
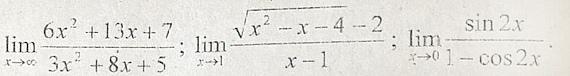
mmb1:
если во втором под корнем x^2-x + 4 то предел есть
но ведь под корнем не плюс, а минус, тогда о чем речь?
речь идет о том, что в учебниках, что в методических указаниях много описок, что в задачах, что в ответах
существует вариант, что есть решение при во втором примере при изменении знака. и даже способ стандартный при этом подходит
существует вариант, что есть решение при во втором примере при изменении знака. и даже способ стандартный при этом подходит
а я и не сомневался в этом, первым делом хотел домножить на сопряженное выражение. О, пользуясь случаем, помогите решить проблемный вопрос. Ни к кому достучаться не могу. https://znanija.com/task/32565991 прошу посмотреть. Возможно я не прав?
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:
Автор ответа:
0
1. надо продифференцировать числитель и знаменатель и потом вычислить предел, производная числителя равна 12х+13, а знаменателя 6х+8, можно еще раз продифференцировать числитель и знаменатель, , в числителе получим 12, в знаменателе 6, значит, предел равен 12/6=2 2.Ко второму примеру применить правило Лопиталя нельзя, т.к. предел отношения двух бесконечно малых величин должен быть равен пределу отношения их производных, если последний предел существует, но это не так. предел не существует.
3. найдем производные числителя и знаменателя, а потом возьмем предел при х стремящемся к к нулю. (2cos2х)/(2sin2x)=ctg2x, а
предел ctg2x, если х устремить к нулю, равен ∞
Похожие вопросы
Предмет: Русский язык,
автор: prostatinae
Предмет: Алгебра,
автор: jsqfatman
Предмет: Английский язык,
автор: rvutep
Предмет: Обществознание,
автор: аделя1232