Предмет: Математика,
автор: ellenasagalp3bwnf
Помогите решить задание 2.5, пожалуйста
Приложения:
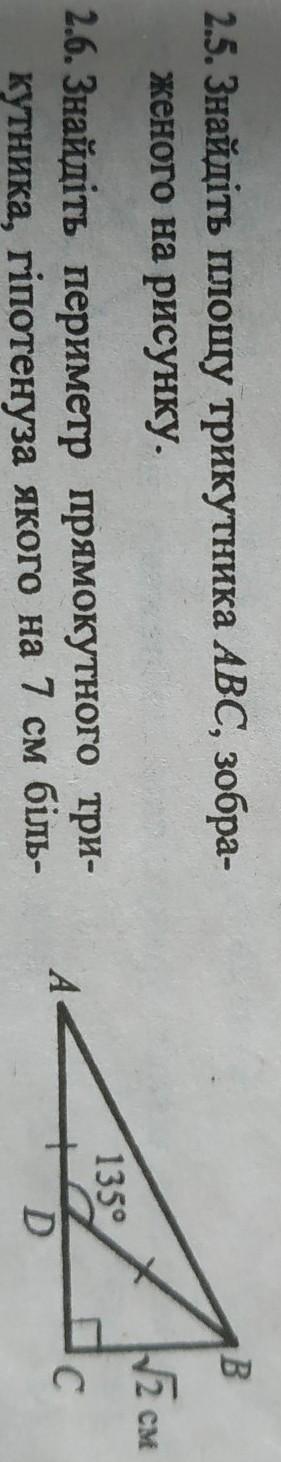
Ответы
Автор ответа:
1
Відповідь:
Покрокове пояснення:
Площа прямокутного трикутника може бути обчислена за формулою:
де a та b - катети.
Невідомий катет АС можна знайти як
Оскільки трикутник BAD - рівнобедрений, то
Знайдемо
Тоді
Отже, площа трикутника буде дорівнювати:
Похожие вопросы
Предмет: Математика,
автор: azizoveduard47
Предмет: Математика,
автор: Sabrina87531
Предмет: Українська мова,
автор: leunov87
Предмет: Геометрия,
автор: IСергейI
Предмет: Геометрия,
автор: danonmi77