Question

Помогите пожалуйста, оооочень нужно и желательно срочно! Даю 100 баллов!!!!

Answer 1

Ответ:

14

Объяснение:

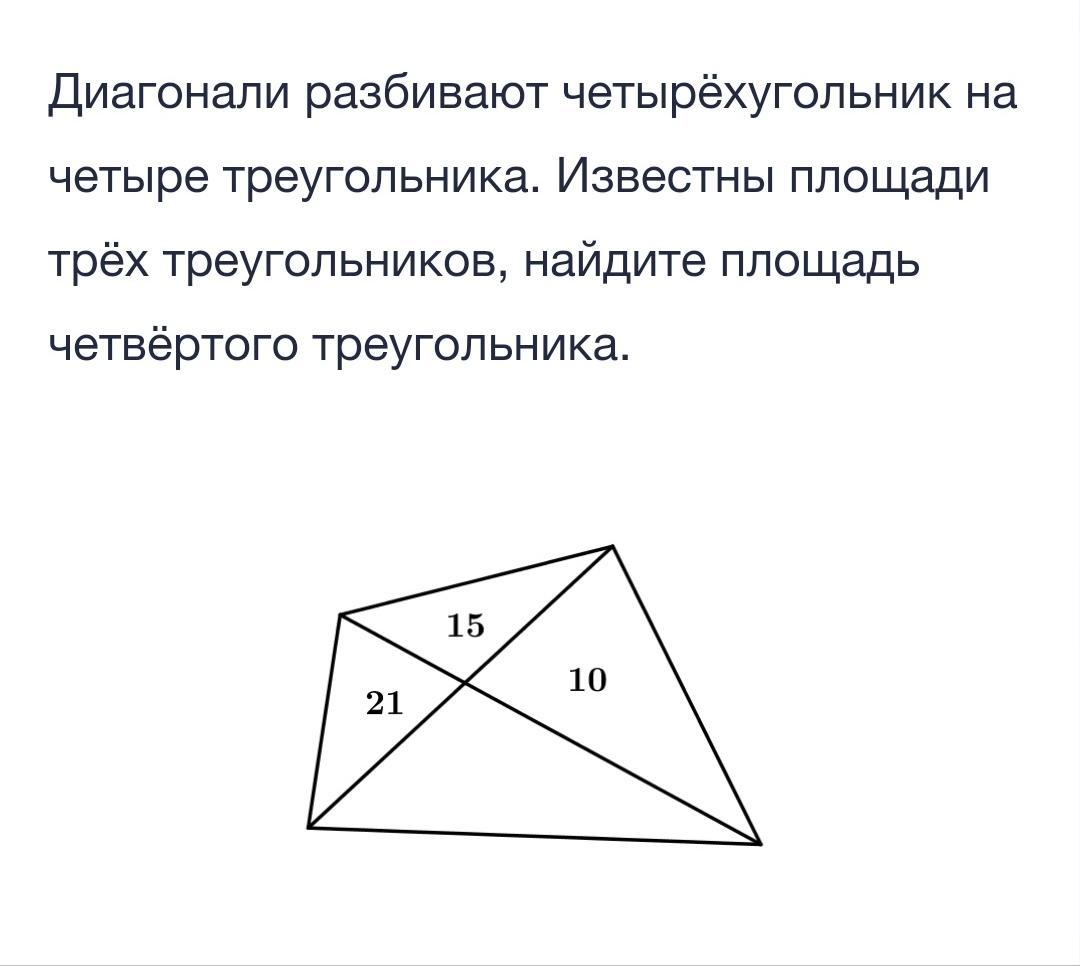
Обозначим данный 4-хугольник как АВСД, т.О - точка пересечения диагоналей.

Имеем:

S(AOB)=(AO*BO*sin∠AOB)÷2; 2*S(AOB)=AO*BO*sinα;

2*S(BOC)=BO*CO*sin∠BOC, при этом ∠BOC=180-∠AOB (смежные или внешний), т.е. sin∠BOC=sin∠AOB ⇒ 2*S(BOC)=BO*CO*sinα;

2*S(COD)=CO*DO*sinα, т.к. ∠COD=∠AOB как вертикальные;

2*S(АOD)=АO*DO*sinα.

Из формул известных площадей получаем систему:

AO*BO*sinα=42

CO*BO*sinα=30

CO*DO*sinα=20

BO=$\frac{30}{CO*sin\alpha }$

$\frac{BO}{DO}=\frac{30}{20}; DO=\frac{2BO}{3}$

$\frac{AO}{CO}=\frac{42}{30}; AO=\frac{42CO}{30}$

2*S(АOD)=АO*DO*sinα=$\frac{42CO}{30}*\frac{2BO}{3}*sin\alpha = \frac{42CO}{30}*\frac{2*30}{3CO*sin\alpha }  *sin\alpha =\frac{84}{3}=28$.

Т.е. площадь неизвестного треугольника равна 28/2=14.