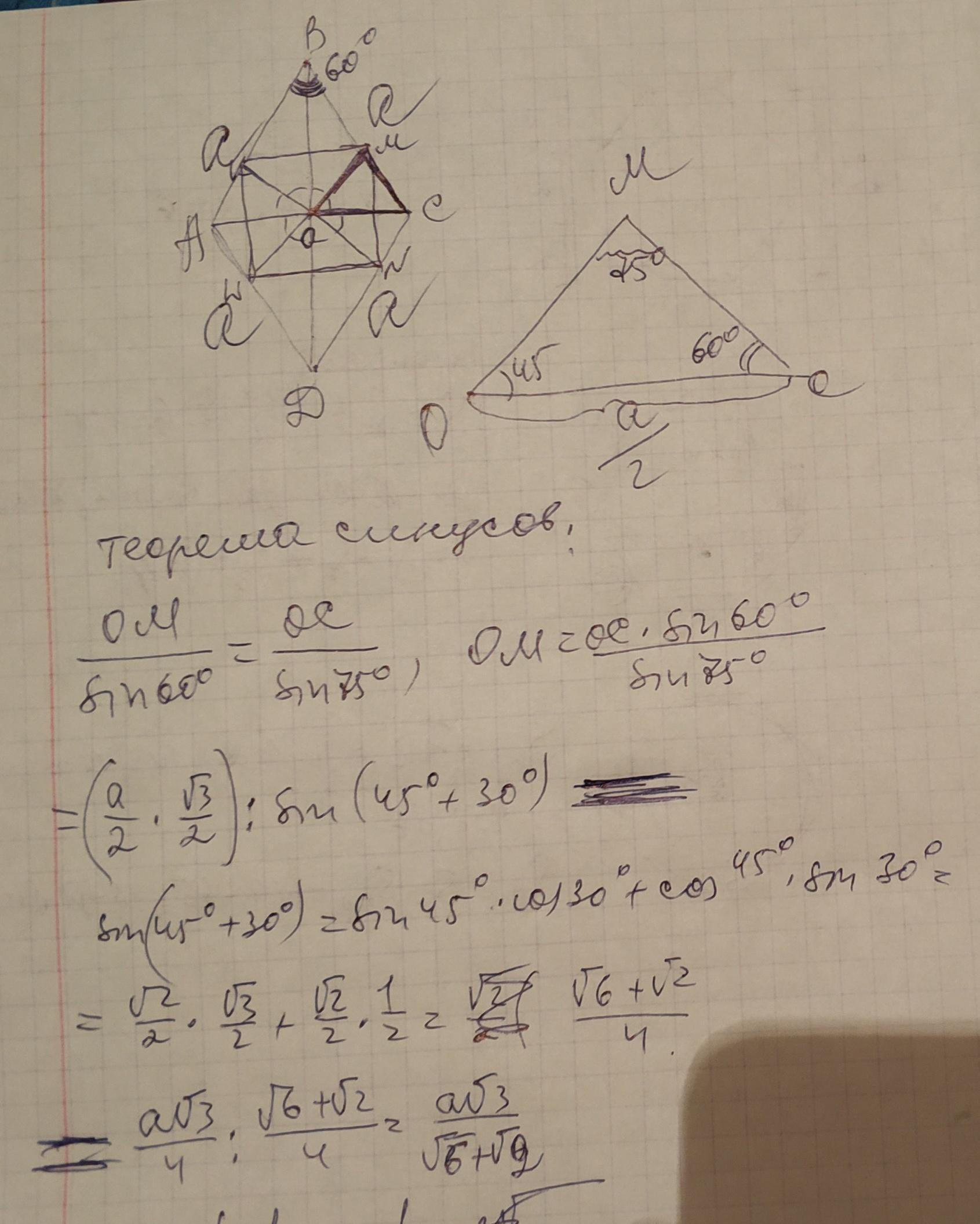
Острый угол ромба равен 60 градусов.В него вписан квадрат.Найдите соотношение периметров ромба и квадрата
Ответы
Вписанный квадрат имеет диагонали под углом 45 градусов к диагоналям ромба.
Примем сторону ромба за 1, а сторону вписанного квадрата за х.
Рассмотрим треугольник из половин диагонали ромба и диагонали квадрата. Известна сторона и 2 угла.
Сторона (это половина диагонали ромба) равна 1*cos(60°/2) = 1*(√3/2) = √3/2. Угол против этой стороны равен 180 - 30 - 45 = 105 градусов.
Половина диагонали квадрата равна х√2/2.
По теореме синусов:
(х√2/2)/sin 30° = (√3/2)/sin 105°.
(х√2/2)/(1/2) = (√3/2)/sin 105°.
Отсюда находим значение стороны вписанного квадрата:
х = √3/(2√2sin 105°) = 0,634.
Ответ: соотношение периметров ромба и квадрата равно
Рр/Рк = 4/(4*0,634) = 1,57735.
Можно перейти к радикалам:
sin 105° = sin (180° - 105°) = sin 75° = sin (30° + 45°) = (1/2)*(√2/2) + (√3/2)*(√2/2) = (√2/4)(1 + √3).
Отсюда х = √3/(1 + √3).
Тогда ответ: Рр/Рк = 4/(4√3/(1 + √3)) = (1 + √3)/√3.
Ответ:
Объяснение: