Предмет: Математика,
автор: bartenevanadezhda
Вычислить площадь фигуры, ограниченной линиями: y=x^2 и y=4x
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
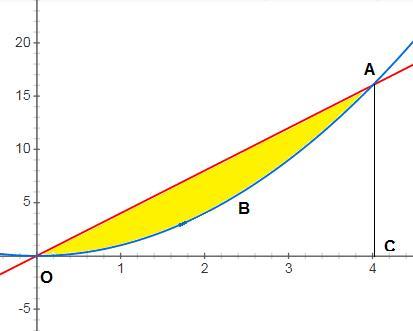
найдем точки пересечения
y=x^2 и y=4x
x²=4x; x²-4x=0; x(x-4)=0; x=0; x=4; y(4)=4*4=16
₄
SOAB=SОАС-SOBAC=16*4/2-∫x²dx=
₄ ⁰
=32-(x³/3)=32-(64/3)=(96-64)/3=32/3=10 2/3 кв.ед
⁰
Приложения:
Автор ответа:
2
1.найдем пределы интегрирования, для чего определим точки пересечения графиков функций y=x² и y=4x
x²=4x; x² - 4x=0; x(x-4)=0; x=0; x=4;
2. найдем определенный интеграл от разности 4х и x², он равен
( 4*х²/2-х³/3) в пределах от нуля до 4
Используя формулу Ньютона -Лейбница, найдем площадь фигуры.
4*4²/2-4*4³/3-0=32-64/3=96/3-64/3=32/3=
10 целых и 2/3 /ед. кв./
Похожие вопросы
Предмет: Математика,
автор: Dovoo777
Предмет: Алгебра,
автор: dariyakovaleva76
Предмет: История,
автор: Аноним
Предмет: Музыка,
автор: Lizulinka
Предмет: Физика,
автор: Dashka089