Предмет: Геометрия,
автор: Rctf
АВ общая касательная к двум касающимся окружностям радиусами 16 и 9 , А и В точки касания. Найдите длину отрезка АВ
Ответы
Автор ответа:
28
Ответ:
АВ = 24 см.
Объяснение:
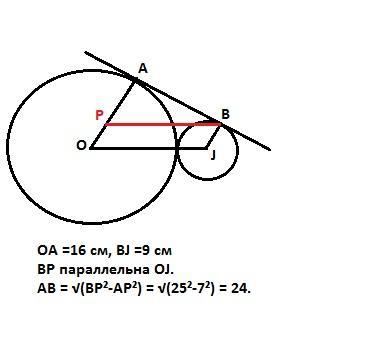
Пусть даны касающиеся окружности с центрами О и J и радиусами ОА и JB соответственно. Радиусы в точках касания перпендикулярны касательной. Следовательно OABJ - прямоугольная трапеция с основаниями ОА и JB. Проведем ВР параллельно прямой OJ.
ВР = OJ = R1+R2 = 25 см. АP = ОА-JB = 16-9 = 7cм.
Тогда в прямоугольном треугольнике АВP катет АВ по Пифагору равен АВ = √(25²-7²) = √576 = 24 см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: lidiber1953
Предмет: Математика,
автор: kristinaflukfelder70
Предмет: Информатика,
автор: Max1mbrain
Предмет: Математика,
автор: Стаснислав2000
Предмет: Математика,
автор: ganja205