исследуйте функцию: y=1/4 x^2(x-4)^2
и постройте её график
Ответы
Исследование функций по схеме:
1. Область определения функции : ограничений нет, х ∈ R.
2. Непрерывность функции, вертикальные асимптоты: разрывов функции нет, значит, функция непрерывна. Поэтому и вертикальных асимптот нет.
3. Точки пересечения функции с осями координат.
С осью Оу при х = 0. Это точка (0; 0).
С осью Ох при у = 0. Надо решить уравнение (1/4) x²(x-4)² = 0.
Получаем 2 точки пересечения: х = 0, х = 4.
4. Четность, нечетность.
f(-х) = (1/4) (-x)²(-x-4)² = (1/4) x²(x+4)² ≠ f(x), ≠ -f(x).
Функция не чётная и не нечётная.
5. Периодичность: не периодическая.
6. Промежутки возрастания, убывания, экстремумы функции.
Находим производную: y' = ((1/4) x²(x-4)²)' = ((1/4) x²(x² - 8x + 16))' =
= (1/4)*(2x*(x² - 8x + 16) + (2x-8)*x²) = (1/4)*(2x³ - 16x² + 32x + 2x³ - 8 x²) =
= (1/4)*(4x³ - 24x² + 32x) = x³ - 6x² + 8x = x(x² - 6x + 8).
Приравниваем её нулю: x(x² - 6x + 8) = 0.
От первого множителя корень х1 = 0.
x² - 6x + 8 = 0. д = 36 - 4*8 = 4. х2 = (6 + 2)/2 = 4, х3 = (6 - 2)/2 = 2.
Имеем 3 критических точки: х = 0, х = 2 и х = 4.
Находим знаки производной на полученных промежутках.
х = -1 0 1 2 3 4 5
y' = -15 0 3 0 -3 0 15.
Видим, что при прохождении через точки х = 0 и х = 4 производная меняет знак с минуса на плюс, то есть это будет минимум, а при прохождении через точку х = 2 – меняет знак с плюса на минус, соответственно это будет максимум.
Промежутки возрастания (y' > 0): (0; 2) ∪ (2; +∞).
Убывания: (-∞; 0) ∪ (2; 4).
7. Промежутки выпуклости, вогнутости, точки перегиба.
Вторая производная равна y'' = 3x² - 12x + 8. Приравняем нулю:
3x² - 12x + 8 = 0. Д = 144 - 4*3*8 = 144 - 96 = 48.
х1 = (12 + √48)/6 = 2 + (2√3/3) ≈ 3,1547,
х2 = (12 - √48)/6 = 2 - (2√3/3) ≈ 0,8453. Это и есть точки перегиба.
8. Наклонные асимптоты: нет.
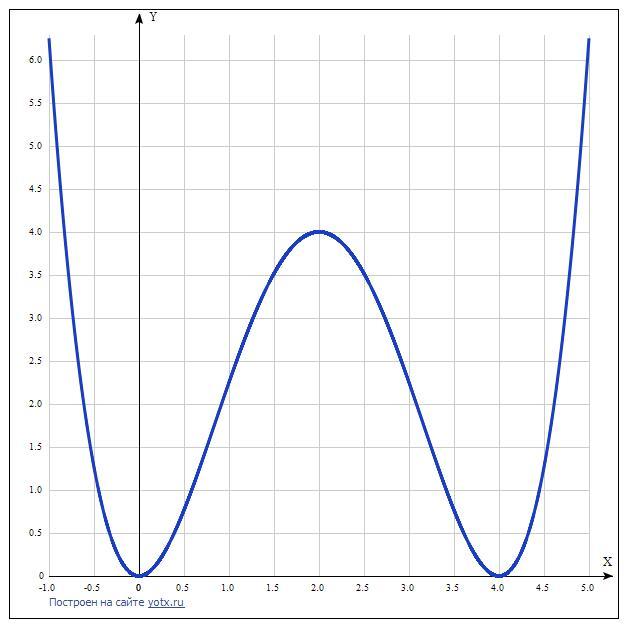
9. Построение графика. Таблица точек:
x y
-1.0 6.25
-0.5 1.27
0 0
0.5 0.77
1.0 2.25
1.5 3.52
2.0 4
2.5 3.52
3.0 2.25
3.5 0.77
4.0 0
4.5 1.27
5.0 6.25