Предмет: Алгебра,
автор: maxsimon91
Помогите вычислить производную функцию в точке x0
Приложения:
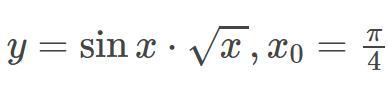
Ответы
Автор ответа:
1
Автор ответа:
0
Производная заданной функции равна:
Подставляем значение х = π/4.
После приведения к общему знаменателю получаем:
После сокращения на корень из 2 получаем ответ:
Похожие вопросы
Предмет: Математика,
автор: alla228fairy
Предмет: Математика,
автор: gontovaairina82
Предмет: Биология,
автор: arinaf081
Предмет: История,
автор: Elya2601
Предмет: Математика,
автор: Аноним