Предмет: Алгебра,
автор: Maria2838
помогите пожалуйста
если нужен рисунок то с ним
я уже в третий раз выкладываю удаляется в чем может быть проблема?
Приложения:
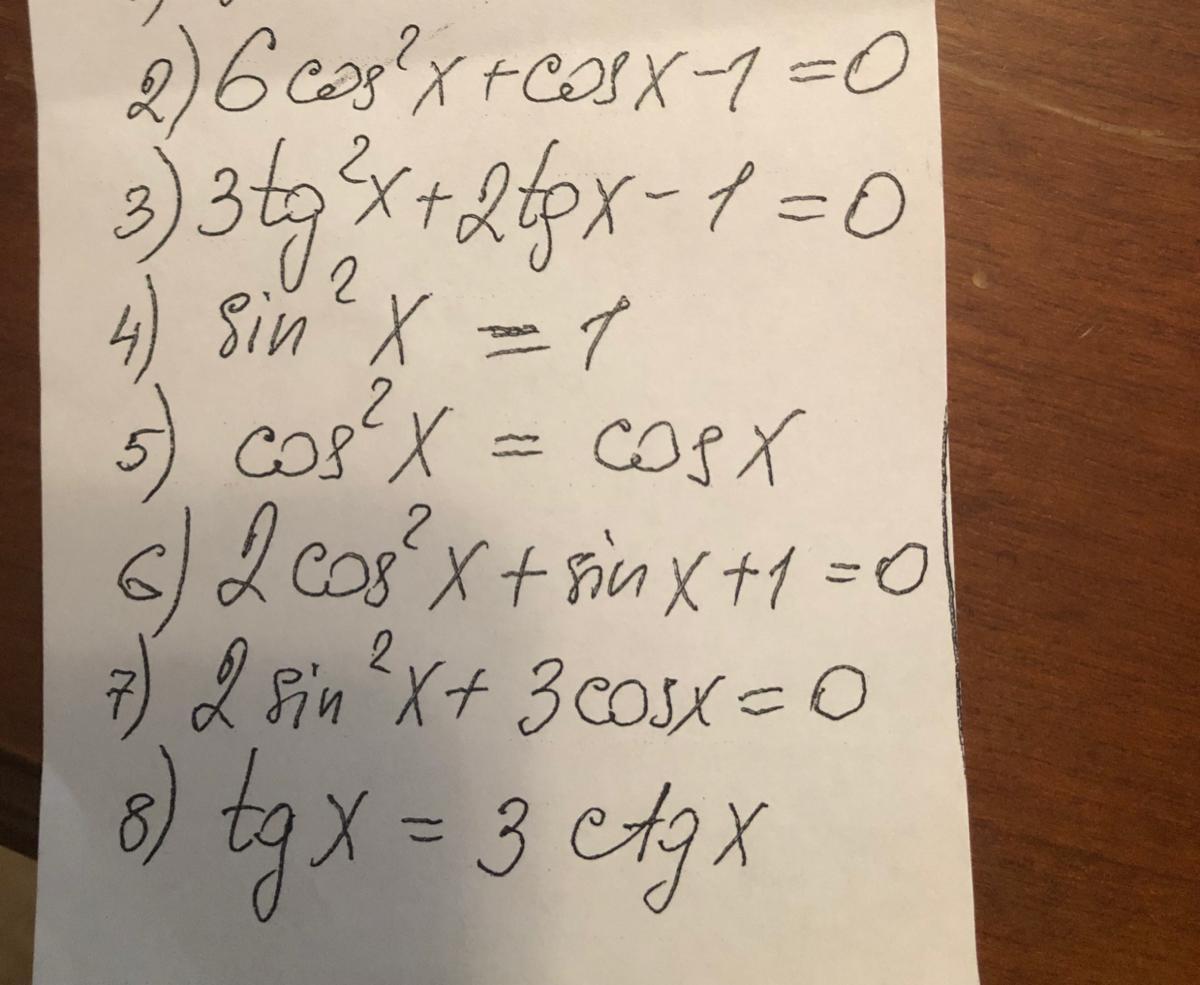
Аноним:
модеры не удаляйте я решу
Ответы
Автор ответа:
1
2)
3)
4)
5)
6)
7)
8)
Похожие вопросы
Предмет: Русский язык,
автор: sophianikolaeva2010
Предмет: Математика,
автор: ivanmaslik2010
Предмет: Математика,
автор: lomakatv89
Предмет: Биология,
автор: Евук
Предмет: Математика,
автор: софия480