триг доказать? ?????
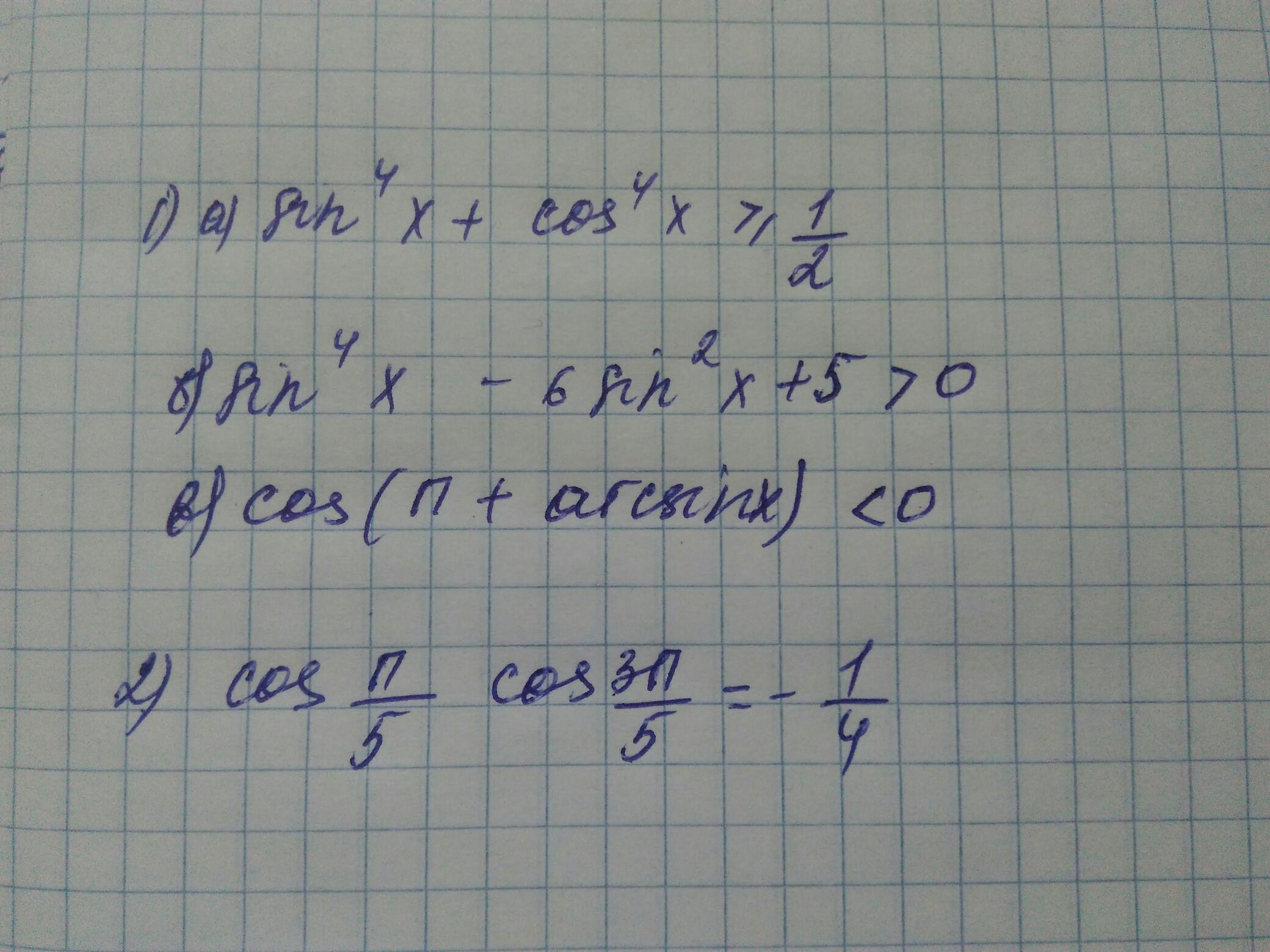
Ответы
Сразу начну с доказательства последнего равенства.
2)Очевидно, что
sin(4pi/5)=sin(pi-pi/5)=sin(pi/5)
2*sin(2*pi/5)*cos(2pi/5)=sin(pi/5)
4*sin(pi/5)*cos(pi/5)*cos*(2pi/5)=sin(pi/5).
4*cos(pi/5)*cos(2*pi/5)=1
cos(pi/5)*cos(2*pi/5)=1/4
Заметим что: cos(2*pi/5)=cos(pi -3pi/5)=-cos(3pi/5)
Откуда: cos(pi/5)*cos(3pi/5)=-1/4
ЧТД.
1)
a) sin^4(x)+cos^4(x)= (sin^2(x)+cos^2(x))^2 --2*sin^2(x)*cos^2(x)= 1-2*(1/2 *sin2x)^2=1-1/2 *sin^2(2x)
Очевидно что: sin^2(2x)<=1
-1/2*sin^2(2x)>=-1/2
1-1/2*sin^2(2x)>=1-1/2=1/2
Вывод: sin^4(x)+cos^4(x)>=1/2
2) sin^4(x)-6sin^2(x)+5
По теореме Виета очевидны корни биквадратного уравнения .(sin^2(x)=t)
t1=1
t2=5
sin^4(x)-6sin^2(x)+5= (sin^2(x)-1)*(sin^2(x)-5)=
(1-sin^2(x))*(4+1-cos^2(x))=
cos^2(x)*(4+cos^2(x))>=0 (тк квадрат число неотрицательное)
Вывод:
sin^4(x)-6sin^2(x)+5>=0
В условии ошибка должно быть строгое неравенство! Достигается когда: cos^2(x)=0, то есть sin^2(x)=1
в) cos(pi+arcsin(x) )
cos(pi+arcsin(x))=-cos(arcsin(x))
Заметим, что область значений arcsin(x) ограничено промежутком:
[-pi/2;pi/2] очевидно ,что косинус от аргумента находящегося на данном промежутке не отрицателен(косинус четная функция).
Тогда сos(arcsin(x))>=0.
-cos(arcsin(x))<=0
Вывод: cos(pi+arcsin(x) )<=0 (и снова ошибка неравенство должно быть строгим!) Выполняется когда x=+-1
делать то , только четвертое триг или все четыри трига ?