Question

Хочу попросить вас написать верное пошаговое решение для задания №14 (ЕГЭ профиль).
Задача: в основании пирамиды лежит равнобедренный треугольник ABC. АВ=АС, SA=BC, SB=SC. Докажите, что SA перпендикулярна ВС.

Answer 1

Ответ:

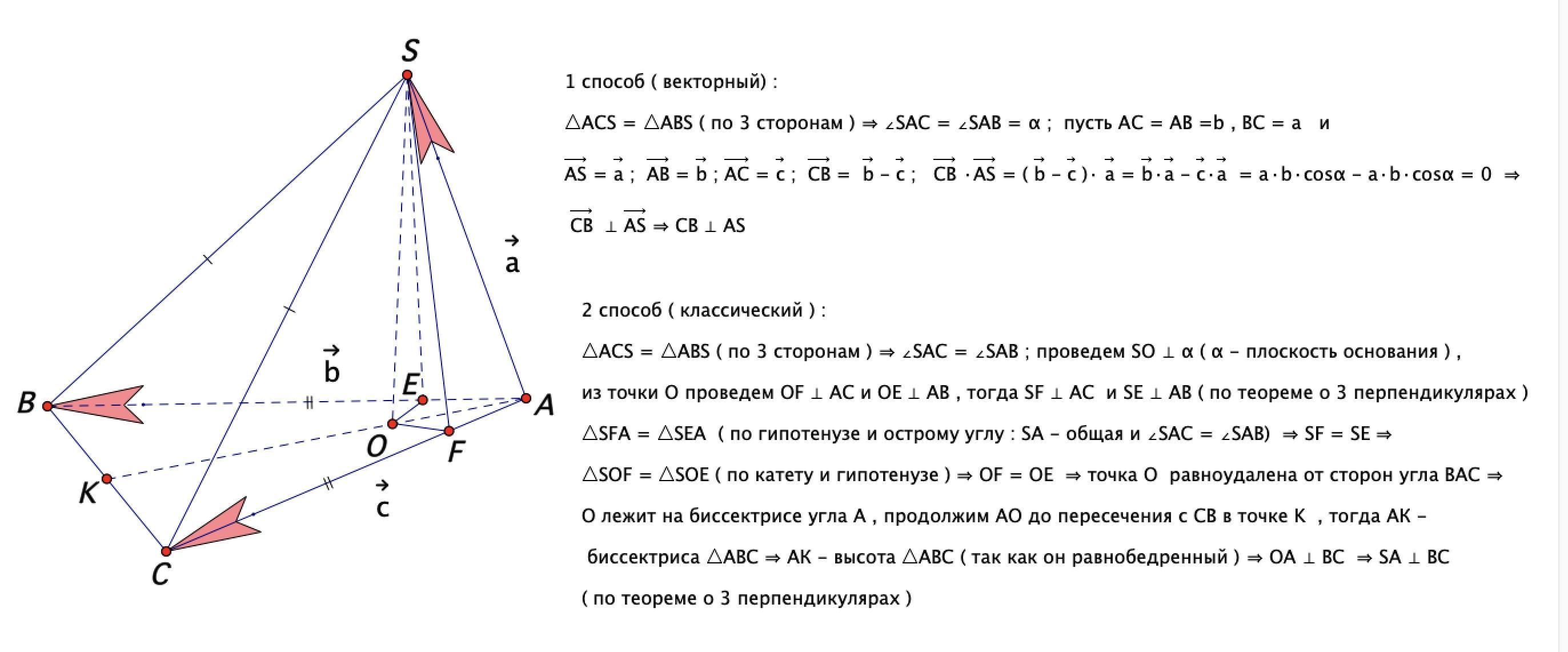
Объяснение:    Решение :  

Answer 2

По условию ∆ВSC и ∆BAC равнобедренные, с общим основанием ВС, значит высо́ты из вершин А и S пересекаются в общей точке (М) на ВС, значит ВС_|_плSMA. Прямая, перпендикулярная плоскости, перпендикулярна любой лежащей на ней прямой, SA принадлежит ∆SMA, следовательно, BC_|_SA, чтд