Question

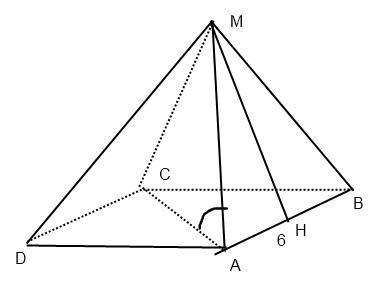
Даю 50 балов за правильный ответ.Срочно!!! Пишу сразу с обозначениями сторон буквами. В правильной четырёхугольной пирамиде (АВСDS) со стороной основания (АВ) равной 6 см и длиной бокового ребра (АS) равной √50 см, найдите косинус угла наклона бокового ребра к плоскости основания и площадь боковой поверхности. Центр основания пирамиды обозначен буквой О. Зарание, спасибо большое))) Попрошу как можно подробнее с косинусом)))

Answer 1

Ответ:

3/5 и 12√41

Объяснение:

Косинус угла

AC=√36+36=6√2

Треугольник MAC – равнобедренный.

cosCAM=(AC/2)/AM=3√2/√50=3/√25=3/5

Площадь боковой поверхности

Sбок=4·(1/2)·MH·AB

MH2=AM2–(AB/2)2

MH=√50–9=√41

Sбок=4·(1/2)·6·√41=12√41

P.S. Мог допустить вычислительную ошибку