Предмет: Алгебра,
автор: mrdiller02
Помогите решить неравенство
Приложения:
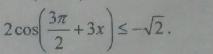
Ответы
Автор ответа:
0
Ответ:
Замечание. После того как Вы упростили неравенство к стандартному, решается оно двумя методами: графически и по окружности.
Похожие вопросы
Предмет: Информатика,
автор: Shhdbdgdudj
Предмет: Информатика,
автор: Shhdbdgdudj
Предмет: Алгебра,
автор: whiteladder13
Предмет: Математика,
автор: при69
Предмет: Математика,
автор: kjkj