Предмет: Алгебра,
автор: stark43
СРОЧНОО!ПОЖАЛУСТА!ОТДАЮ ВСЁ ЧТО ЕСТЬ! ЗАДАНИЕ НА ФОТКЕ!
Приложения:
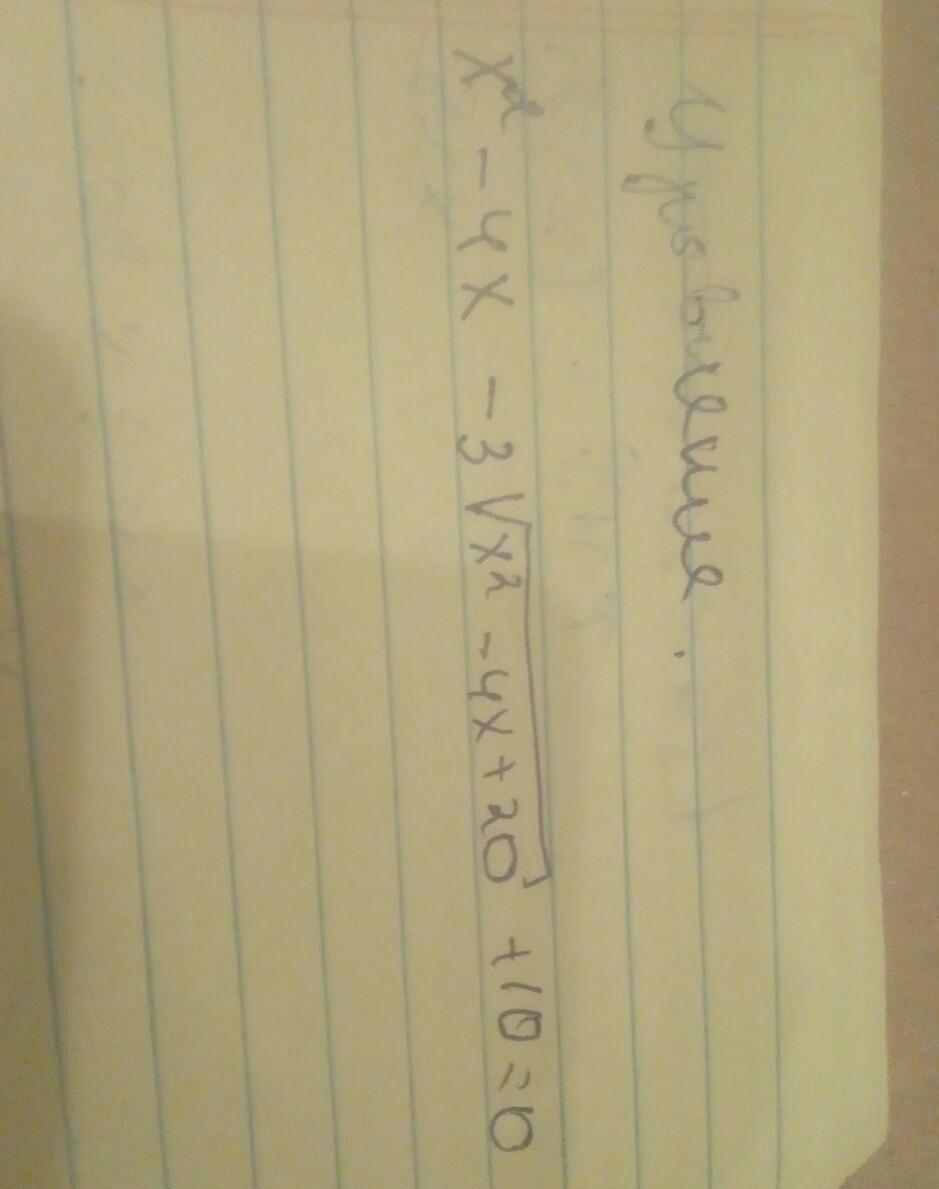
Ответы
Автор ответа:
1
Ответ:
Замечание. Это уравнение можно решить графически, построив графики функций и
, и найти точки пересечения графиков.
Похожие вопросы
Предмет: Английский язык,
автор: Danielabauerrr
Предмет: ОБЖ,
автор: andreychikishev888
Предмет: Информатика,
автор: pollianna2019
Предмет: Математика,
автор: 567804саша