Предмет: Математика,
автор: YkharitonovaM
Найдите частное решение дифференциального уравнения с разделяющимися переменными
Приложения:
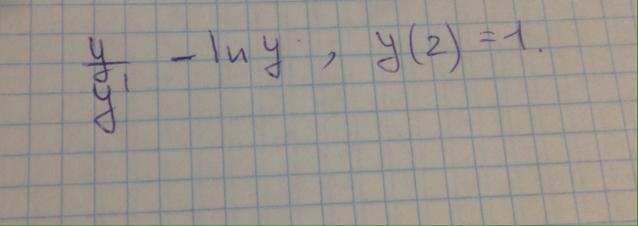
HSS9860:
Непонятно, где находится знак "равно"...
Как бы это уравнение с начальным условием
И его потом надо будет приравнять к 0
И его потом надо будет приравнять к 0
Да
А равно должно быть там, где минус.
Не правильно записано
А равно должно быть там, где минус.
Не правильно записано
Ответы
Автор ответа:
0
- общее решение
- частное решение
В последней строке квадрат над логарифмом не доставили...
Точно..
Похожие вопросы
Предмет: История,
автор: nikitavedkal3
Предмет: Химия,
автор: voitovskayuliana
Предмет: Обществознание,
автор: bitukovaleksandor
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Ирина090505