Предмет: Геометрия,
автор: slowmode2
Геометрия 10 класс с решением пожалуйста 18 баллов
Приложения:

Ответы
Автор ответа:
2
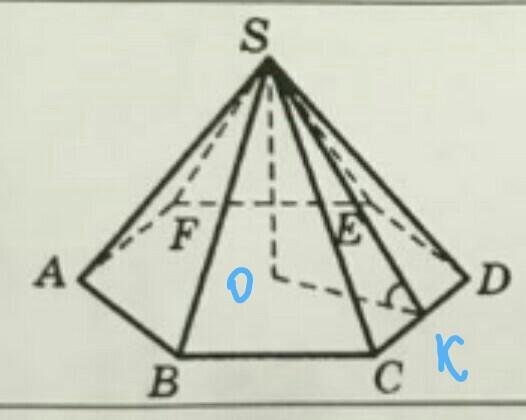
Высота в пирамиде - SO.
1. Рассм. треуг. SOK: угол О=90 градусов, угол К=угол S=45 градусов => треуг. прямоугольный и равнобедренный, т.е. ОК=SO=8 см. По т. Пифрагора найдем SK:
2. OK - радиус вписанной окружности в правильный шестиугольник, который по формулам равен
где а - сторона шестиугольника.
Из этого выражения найдем а:
3. Рассм. треуг. SCD: он равнобедренный. Sscd=
4. Sscd=Ssde=Ssef=Ssaf=Ssab=Ssbc
Sбок=Sscd+Ssde+Ssef+Ssaf+Ssab+Ssbc= Sscd×6=
5. Вычисления для ответа:
Ответ: 768 см^2.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: www7067
Предмет: Информатика,
автор: Python444
Предмет: Биология,
автор: soychukveronika
Предмет: Химия,
автор: Karina3215
Предмет: Биология,
автор: чоторо