Очень нужно решить данный интеграл, помогите!
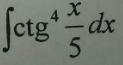
Ответы
интеграл буду писать S
сtg = cos / sin
csc = 1/ sin
ctg^2 = csc^2 - 1
S x^n dx = x^(n+1)/(n+1) + c
S C dx = Cx + C1
S csc²(x) dx = - ctg (x) + C
S ctg^4(x/5) dx =
= (замена u=x/5 dx=5du) =
= 5 S ctg^4(u) du = 5 S ctg^2(u)*ctg^2(u) du = 5 S ctg^2(u)*(csc^2(u) - 1)du = 5 S (ctg^2(u)csc^2(u) - ctg^2(u)) du = 5 S ctg^2(u)*csc^2(u) du - 5 S ctg^2(u) du = ......(1)
..... получили разницу двух интегралов
решаем второй S ctg^2(u) du = S (csc^2(u) - 1) du = S csc^2(u) du - S du = (два табличных) = -ctg(u) - u + C
решаем первый S ctg^2(u)*csc^2(u) du = { замена v = ctq(u) dv = - 1/csc^2(u) } = - S v^2 dv = -v^3/3 = - ctg^3(u)/3 + C
......(1) итак
- 5ctg^3(u)/3 - 5*(-сtg(u) - u) + C = { делаем обратную замену u = x/5} = 5*( x/5 + ctg(x/5) - ctg^3(x/5)/3) + C
=====================
понятно и нравится ставь лайк и лучший