Question

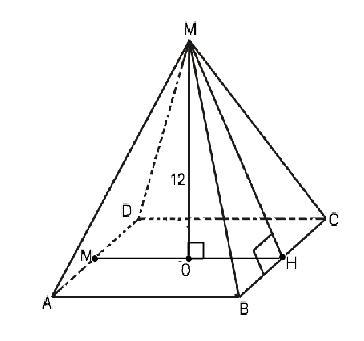
дана правильная четырехугольная пирамида с высотой 12 см объем пирамиды 4096 см^3 вычислите площадь боковой поверхности пирамиды

Answer 1

Ответ: 1280 см²

Объяснение:

Формула объема пирамиды V=h•S/3, где S - площадь основания пирамиды, h - её высота ⇒

S=3•V/h  S=3•4096/12=1024 см²

Пирамида правильная, следовательно, её основание квадрат с площадью  S=a² ⇒ a=√1024=32 см

Площадь боковой поверхности правильной пирамиды равна произведению апофемы на полупериметр основания. Ѕ(бок)=МН•Р(ABCD):2

Апофему МН найдем из прямоугольного ∆ МОН, где МО - высота, ОН - половина средней линии МН в ☐АВСD.  МН=АВ=32, ОН=32:2=16 см

По т.Пифагора МН=√(12²+16²)=20 см

Ѕ(бок)=20•(32•4):2=1280 см²