Решите данное неравенство :
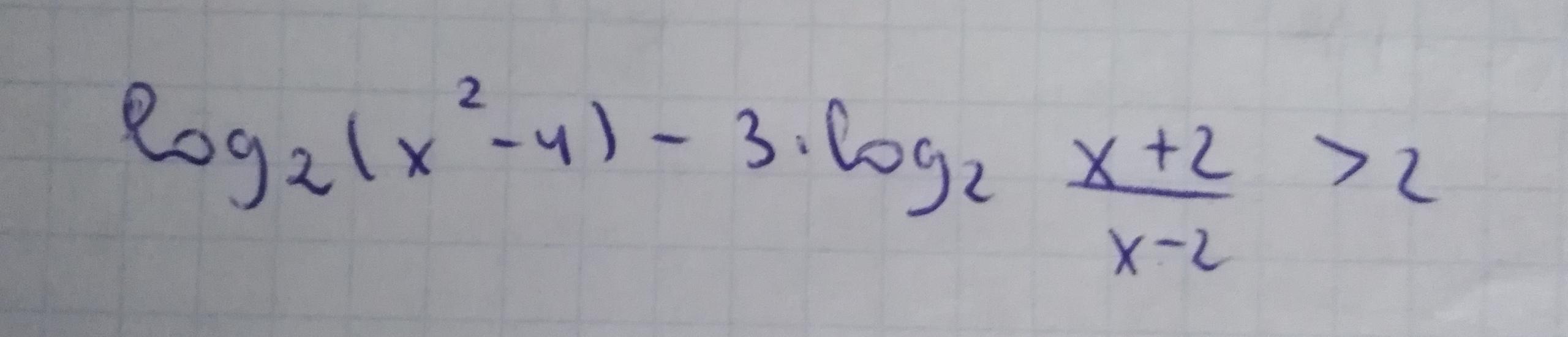
Ответы
Учтём, что х² - 4 = (х -2)(х +2).
log₂(x -2) + log₂(x +2) -3log₂(x+2) +3log₂(x -2) >2
4log₂(x -2) -2log₂(x +2) > 2
2log₂(x -2) - log₂(x +2) > 1
2log₂(x -2) - log₂(x +2) > log₂2
С учётом ОДЗ составим систему неравенств:
х - 2 > 0, ⇒ x > 2
x + 2 > 0, ⇒ x > -2
(x - 2)²/ (x +2) > 2, ⇒ (x - 2)²/ (x +2) - 2 > 0,
Решаем 3-е нер-во методом интервалов.
(x - 2)²/ (x +2) - 2 > 0,
(х² -4х +4 -2х -4)/(х +2) >0
(x² -6x)/(х +2) > 0
x² - 6x = 0
корни 0 и 6
х +2 = 0
х = -2
-∞ (-2) (0) (6) +∞
+ + - + знаки x² - 6x
- + + + знаки х +2
IIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIII это решение (x² -6x)/(х +2) > 0
Теперь общее решение:
-∞ (-2) (0) (2) (6) +∞
IIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIII это решение (x² -6x)/(х +2) >0
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII это х > -2 (ОДЗ)
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII это х > 2 (ОДЗ)
Ответ: х∈(6; +∞)