Question

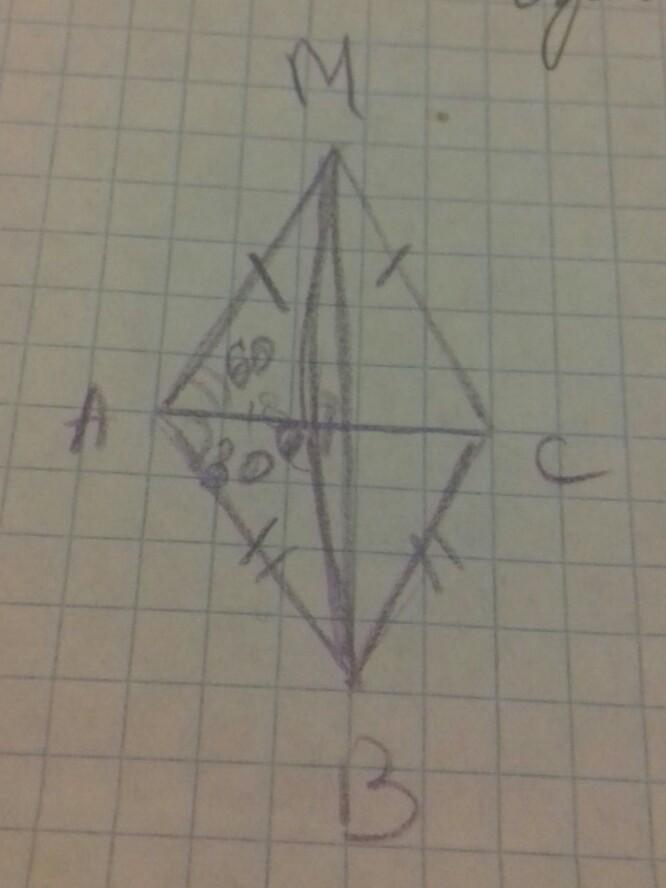
∆ABC и ∆АMC равнобедренные с основанием АС=36м , а углы при их основаниях 30° и 60°соответственно.Найдите угол между плоскостями треугольников , если ВМ=6√21м.

Answer 1

1. Рассмотрим треуг. АОВ: уголА=30 градусов; т.к. ВО - высота, то треуг. АОВ - прямоугольный, АО=ОС=18 см.

Пусть ВО=х см.

$tg30 = \frac{x}{18} \\ x = tg30 \times 18 = \frac{ \sqrt{3} }{3} \times 18 = 6 \sqrt{3}$

2. Рассм. треуг. АМО: уголА=60 градусов; т.к. треуг. АМС равнобедренный, то МО - высота и треуг. АМО - прямоугольный.

Пусть МО=у см.

$tg60 = \frac{y}{18} \\ y = tg60 \times 18 = 18 \sqrt{3}$

3. Рассмотрим треуг. МОВ:

Пусть МВ=а, МО=b, ВО=с, угол МОВ= альфа, тогда по т. косинусов:

${a}^{2} = {b}^{2} + {c}^{2} - 2bc \cos( \alpha ) \\ 36 \times 21 = 324 \times 3 + 36 \times 3 - 2 \times 18 \sqrt{3} \times 6 \sqrt{3} \times \cos( \alpha ) \\ 756 = 972 + 108 - 648 \times \cos( \alpha ) \\ - 648 \cos( \alpha ) = - 324 \\ \cos( \alpha ) = \frac{ - 324}{ - 648} \\ \cos( \alpha ) = 0.5$

Значит, угол МОВ=60 градусов.

Ответ: 60 градусов.