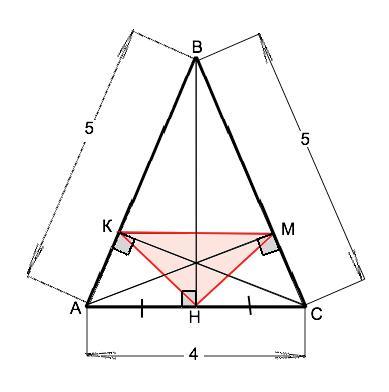
Треугольник ABC - равнобедренный, AB=BC=5, AC=4.
Найдите периметр ортотреугольника
Ответы
Ответ: 6,72
Объяснение: Ортотреугольником называют треугольник, вершинами которого являются основания высот некоторого треугольника.
* * *
На рисунке точки К, М и Н - основания высот треугольника АВС. ⇒ ∆КМН - его ортотреугольник.
Решение:
Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой. ⇒ АН=СН=4:2=2.
Прямоугольные ⊿ АКС=⊿ СМА по равному острому углу ( ∠А=∠С как углы при основании равнобедренного треугольника) и общей гипотенузе АС.
Медианы прямоугольных треугольников равны половине гипотенузы.. КН=МН=4:2=2. Следовательно, АН=КН, СН=МН, – ∆ АКН и ∆ СМН равнобедренные, при этом углы при их основаниях равны углам при основании ∆ АВС. Поэтому
∆ АКН и ∆СМН подобны ∆ АВС.
Из подобия следует НС:ВС=МС:АС ⇒ 2:5=МС:4, откуда МС=8/5=1,6
ВК=ВМ=ВС-СМ=5-1,6=3,4
∆ КВМ~∆ АВС ( оба равнобедренные с общим острым углом В) ⇒
ВК:АВ=КМ:АС ⇒ КМ=3,4•4:5=2,72
Р(КМН)=КМ+КН+МН=2,72+2+2=6,72 ( ед. длины)