Предмет: Математика,
автор: izabella9
Помогите пожалуйста Помогите
Приложения:
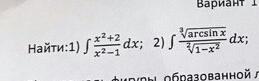
Ответы
Автор ответа:
2
1) Метод неопределенных коэффициентов
Система
{ A + B = 0
{ A - B = 3
Складываем уравнения
2A = 3
A = 1,5
B = -1,5
2) Метод замены переменной
izabella9:
Помогите мне пожалуйста с уравнениями в профиле
Похожие вопросы
Предмет: Математика,
автор: hon29082018
Предмет: Алгебра,
автор: olgamakeeva05
Предмет: Математика,
автор: nerpy
Предмет: Алгебра,
автор: Malishka2518
Предмет: Алгебра,
автор: ЖаннаРустам