Question

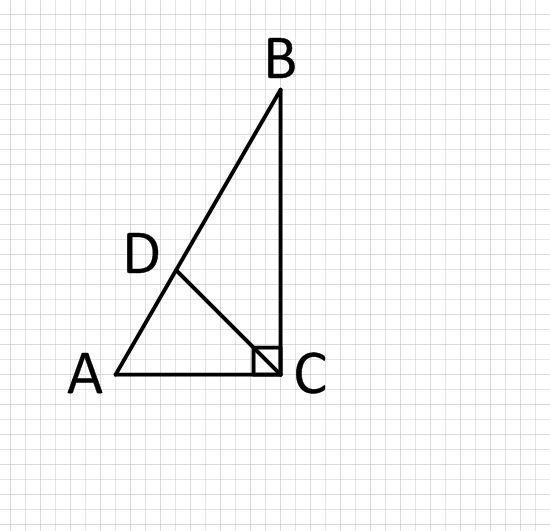
В прямоугольном треугольнике ACB(угол C = 90°) проведена высота CD. Гипотенуза AB равна 8 см, угол CBA =30°. Найдите BD.​

Answer 1

Ответ:

8√3/(1+√3) см

Объяснение:

По свойству прямоугольных треугольников, катет лежащий напротив угла в 30 градусов равен половине гипотенузы

AC=AB/2=8/2=4 см

По теореме Пифагора найдет третью сторону прямоугольного треугольника ACB:

AB²=AC²+BC²

BC²=AB²-AC²

BC=√(AB²-AC²)=√(64-16)=√48 =4√3 см

Биссектриса делит противоположную сторону треугольника пропорционально прилегающим сторонам:

AD/BD = AC/BC

учитывая, что

AD=AB-BD

получаем:

(AB-BD)/BD = AC/BC

AB/BD-BD/BD=AC/BC

AB/BD-1=AC/BC

AB/BD=AC/BC+1

BD=AB:(AC/BC+1)

BD=8:(4/(4√3)+1)=8:1/√3+8=8√3/(1+√3) см