Предмет: Математика,
автор: izabella9
Помогите Пожалуйста Решить...
Приложения:

Ответы
Автор ответа:
8
Ответ:
интеграл===================================
Пошаговое объяснение:
Приложения:
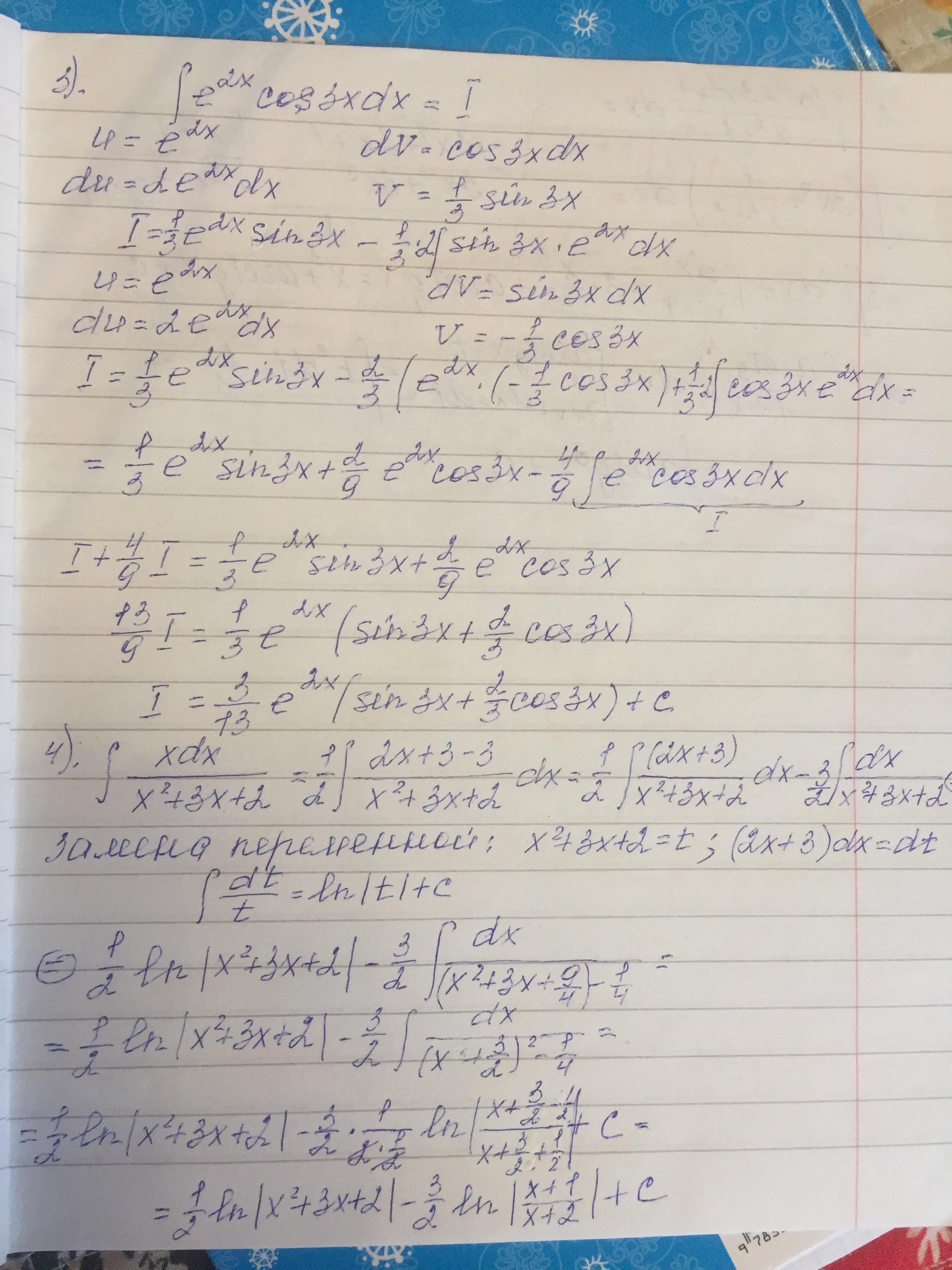
natalyabryukhova:
В конце поправила
Спасибо
а что такое I
в решение 1 примера
модуль
ААА. Это интеграл)
Автор ответа:
2
3) Решается по частям
Снова по частям
Это интегральное уравнение. Обозначим \int {e^{2x}cos(3x)} \, dx =I.
4) Решается методом неопределенных коэффициентов.
x(A+B) + (2A+B) = x
{ A + B = 1
{ 2A + B = 0
Из 2 уравнения вычитаем 1 уравнение
A = -1; B = 2
Что такое I
???
Это я условно обозначил Интеграл, что бы не писать всю формулу.
поняла)
спасибо
Похожие вопросы
Предмет: Химия,
автор: kolapro66
Предмет: Геометрия,
автор: korakovcevegor10
Предмет: Геометрия,
автор: alenaguzova1
Предмет: Математика,
автор: ирина1286
Предмет: Алгебра,
автор: polinka180