Предмет: Математика,
автор: NewTechnology
Найдите неопределённый интеграл подробно:
Приложения:
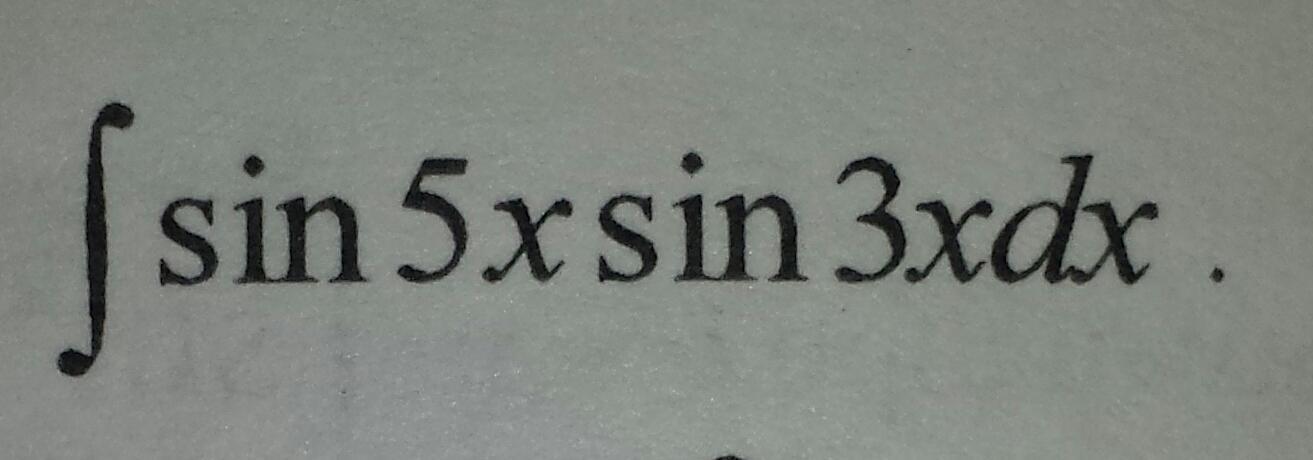
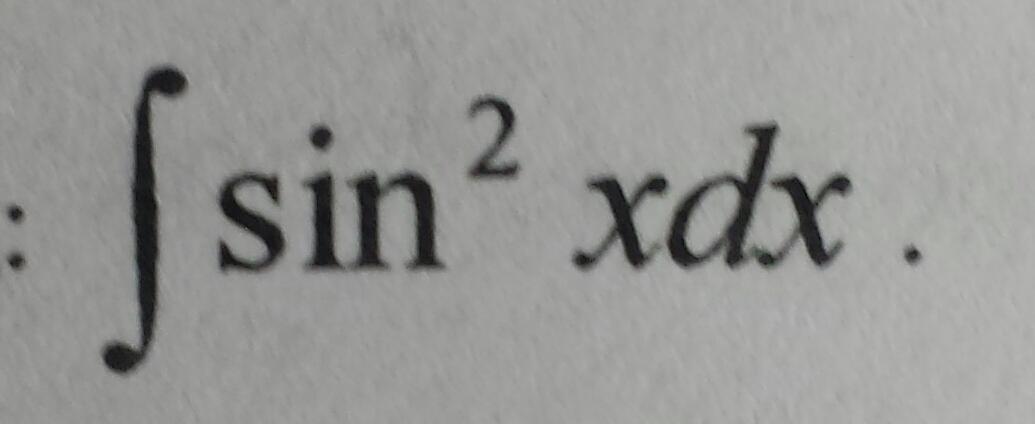
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: nerpy
Предмет: Геометрия,
автор: Аноним
Предмет: Химия,
автор: rahimzansahmetov
Предмет: История,
автор: Даня11211
Предмет: Математика,
автор: Иванованатальяиндич