Предмет: Алгебра,
автор: FanerC
Помогите решить 2^(x^2-4x+6)=cos п x+3
Приложения:
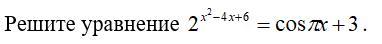
Ответы
Автор ответа:
0
Дано уравнение 2^(x²-4x+6)=cos(πx)+3.
Исследуем левую часть его.
Показатель степени числа 2 - квадратичная функция , график которой - парабола ветвями вверх. Минимум этой функции в вершине параболы.
хо = -в/2а = 4/(2*1) = 2,
уо = 2² - 4*2 + 6 = 4 - 8 + 6 = 2.
Итого левая часть при основании больше 1 в точке х = 2 имеет минимум со значением 2² = 4.
Теперь перейдём к правой части.
Функция косинуса имеет пределы +-1, а в сумме с 3 это от 2 до 4.
При сопоставлении двух частей видим, что единственная точка их равенства это значение х = 2.
Можно проверить:2^(2^2 - 4*2 + 6) = 2^2 = 4.
cos(2π) + 3 = 1 + 3 = 4.
Равенство соблюдено.
Ответ: х = 2.
Похожие вопросы
Предмет: История,
автор: daragolosapova0459
Предмет: Литература,
автор: valia1711
Предмет: Обществознание,
автор: camistjdeffy
Предмет: Алгебра,
автор: llina2
Предмет: Литература,
автор: Мишаня111111111