Предмет: Алгебра,
автор: volter990
Помогите, пожалуйста, решить уравнение.
sqrt (x^2+x+12)/(4x-3)<=0
Приложения:
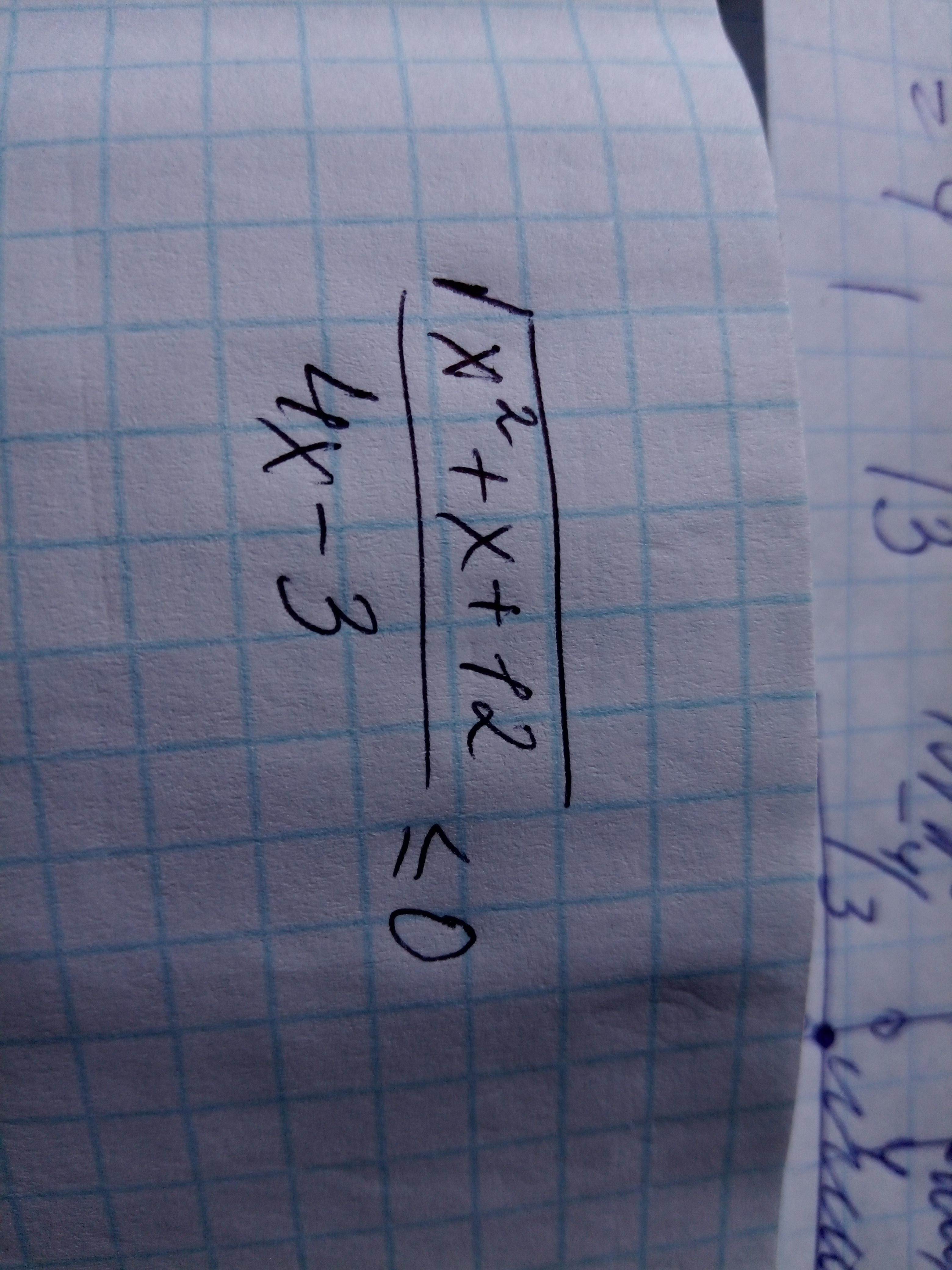
maksimcat:
задайте вопрос по-другому: КОНТРОЛЬНЫЕ НЕЛЬЗЯ РЕШАТЬ
Простите, больше не буду писать так, да и она последняя в жизни
числитель больше нуля при любом х, знаменатель меньше нуля , х<3/4
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Українська мова,
автор: kazatin23122018
Предмет: Биология,
автор: vladislavatokarchuk
Предмет: История,
автор: мимими29
Предмет: Математика,
автор: софи104