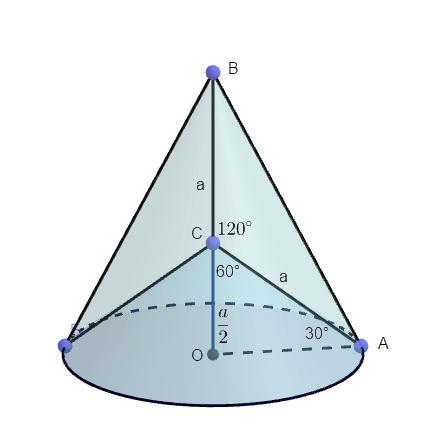
Равнобедренный треугольник с углом при вершине 120° и боковой стороной а вращается вокруг боковой стороны. Определить объем тела вращения
Ответы
При вращении заданного треугольника вокруг боковой стороны получается тело вращения, состоящее из конуса с образующей AB (основание Δ ABC) и конуса с образующей СА (боковая сторона Δ ABC). Оба конуса имеют равное основание – окружность радиуса OA. Радиус окружности основания конусов – перпендикуляр, опущенный из вершины A ΔABC на ось вращения.
Объем тела вращения (V) будет равен разности объемов большого (V₁) и малого (V₂) конусов. V = V₁ – V₂ ;
Объем конуса V = 1/3 * SoH; So – площадь основания, H – высота конуса.
В прямоугольном треугольнике ΔAOC <ACO = 60⁰ , так как он смежный с заданным углом ΔABC <ACB = 120⁰ (сумма смежных углов = 180⁰). Тогда <OAC = 180⁰ – 90⁰ – 60⁰ = 30⁰. Боковая сторона ΔABC AC является гипотенузой ΔAOC = a. Катет, лежащий против угла 30 равен половине гипотенузы. Высота малого конуса CO = a/2.
Найдем радиус окружности по т.Пифагора из ΔAOC: OA = R; R² = a²– (a/2)² = a² – (a²/4) = 3a²/4; R =a*√3/2;
Площадь основания So=πR² = 3πa²/4;
Высота большого конуса H = a+a/2 = 3a/2;
Объем большого конуса V₁ = 1/3 * 3πa²/4 * 3a/2 = 3πa³/8;
Объем малого конуса V₂ = 1/3 * 3πa²/4 * a/2 = πa³/8;
Объем тела вращения V = V₁ – V₂ = 3πa³/8 - πa³/8 = 2πa³/8 = πa³/4.