Question

СРОЧНО 40 БАЛОВ

Стороны параллелограмма равны 6см и 7см, угол между ними 60 градусов . Найти высоты параллелограмма.

Answer 1

${6}^{2} = {x}^{2} + {3}^{2} \\ 36 = {x}^{2} + 9 \\ {x}^{2} = 27 \\ x = \sqrt{27 } = 3 \sqrt{3}$

Answer 2

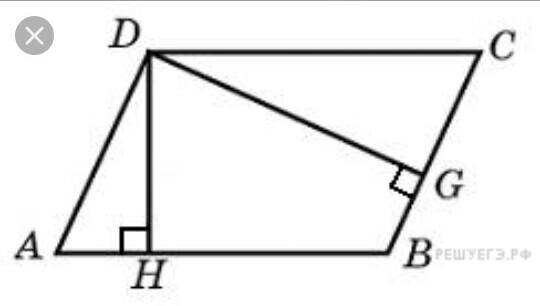
Дано: АД=6 см, АВ=7 см, уголА=60 градусов.

Найти: ДН, ДG.

Решение:

BC=AD=6 см.

Рассм. треуг. АДН: угол АНД=90 градусов, АД=6 см, уголА=60 градусов. По sinА найдем ДН:

$\frac{ \sqrt{3} }{2} = \frac{ x}{6} \\ x = \frac{6 \sqrt{3} }{2} \\ x = 3 \sqrt{3}$

Sabcd=AB×DH=BC×DG.

$s = 3 \sqrt{3} \times 7 = 21 \sqrt{3}$

DG=S/BC.

$\frac{21 \sqrt{3} }{6} = 3.5 \sqrt{3}$

Ответ:

$3.5 \sqrt{3}$ см, 3√3 см.